Question

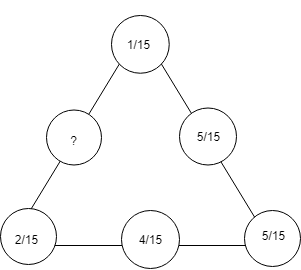
What should be placed in the empty space? So that the sum of the fractions on each side of the triangle is the same?

\[
  \,A)\,\dfrac{7}{{15}} \\
  \,B)\,\dfrac{9}{{15}} \\
  \,C)\,\dfrac{6}{{15}} \\
  \,D)\,\dfrac{8}{{15}} \\
 \]

Answer 1

Hint: As per the given question, first find the sum of fraction on sides of the triangle on known values, then find the empty space by subtracting the unknown sides from the sum of sides of triangle.

Formula used: The side of the triangle should be calculated as side 1 $ + $side 2 $ + $side 3 = sum of the side of triangle. To find anyone on either side of the triangle, put the unknown side of the triangle on the left side, side 2 $ = $sum of the side of triangle $ - $side 1 $ + $side 3.

Complete step-by-step answer:
Given that, in the diagram six points are present in the triangle. In that only five points are given in the question. We want to find the empty space. The hint is given in the question that the sum of the fractions on each side of the triangle is the same.
To find the empty space in the triangle, we want to find the sum of fraction on each sides of the triangle:
By considering the right side of the triangle, the fraction points are $\dfrac{1}{{15}}\,,\,\dfrac{5}{{15}}$ and $\dfrac{5}{{15}}$
   Sum of right side of triangle $ = \,\dfrac{1}{{15}}\, + \,\dfrac{5}{{15}}\, + \,\dfrac{5}{{15}}\,$
Taking $15$as common denominator, the equation becomes:
    Sum of right side of triangle $ = \,\dfrac{{1\, + \,5\, + \,5}}{{15}}$
The sum of the right side of the triangle is$\dfrac{{11}}{{15}}$.
By considering the bottom side of the triangle, the fraction points are $\dfrac{2}{{15}}\,,\,\dfrac{4}{{15}}$ and $\dfrac{5}{{15}}$
Sum of bottom side of triangle $ = \,\dfrac{2}{{15}}\, + \,\dfrac{4}{{15}}\, + \,\dfrac{5}{{15}}\,$
Taking $15$ as common denominator, the equation becomes:
Sum of bottom side of triangle $ = \,\dfrac{{2\, + \,4\, + \,5}}{{15}}$
The sum of the bottom side of the triangle is$\dfrac{{11}}{{15}}$.
Thus, on each side of the triangle we must have the value$\dfrac{{11}}{{15}}$.
To find the empty space in the triangle, we have to solve the problem as follows:
Left side of the triangle = side 1 + side 2 + side3
Substitute sum of the triangle on side to the left side of the triangle:
Thus, side 1 + side 2 + side 3 $ = \,\dfrac{{11}}{{15}}$
Substitute the values of side 1$ = \,\dfrac{1}{{15}}$, side 2 $ = \,x$ and side 3$ = \,\dfrac{2}{{15}}$ in the equation as follows:
$\Rightarrow$ $\dfrac{1}{{15}}\, + \,x\, + \,\dfrac{2}{{15}}\, = \,\dfrac{{11}}{{15}}$
Calculate the two sides:
$\Rightarrow$ $\dfrac{3}{{15}}\, + \,x\, = \,\dfrac{{11}}{{15}}$
For substituting the value of $x$, get $\dfrac{3}{{15}}$to right side of the equation as follows:
$\Rightarrow$ $x\, = \,\dfrac{{11}}{{15}}\, - \,\dfrac{3}{{15}}$
In the above equation, $15$is the denominator for both values, so take it as common value for the equation
$\Rightarrow$ $x\, = \,\dfrac{{11\, - \,3}}{{15}}$
Calculating the value of $x$ as:
$\Rightarrow$ $x\, = \,\dfrac{8}{{15}}$
Thus, the value of side 2 is $\dfrac{8}{{15}}$.
The option $\,D\,)\,\dfrac{8}{{15}}$is the correct answer for the empty space.

Note: Before finding the empty space value, we have to find the sum of fraction on right side of triangle and bottom side of the triangle.