Question

What is the perimeter and the area of a square with $12ft.$ side?

Answer 1

Hint: We know that the perimeter of a square having a side $a$ units can be found by the formula $2\left( a+a \right)=4a$ and we also know that the area of a square with a side $a$ units can be found by the formula $a\times a={{a}^{2}}.$

Complete step by step solution:
Let us consider the given square with $12ft.$ side.
We are asked to find the perimeter and the area of the given square.
Let us suppose that we have a square with a side of $a$ units. Then we can find the perimeter using the formula $2\left( a+a \right)=4a$
So, we can find the perimeter of the given square using the above formula.
So, the side of the given square is $a=12ft.$

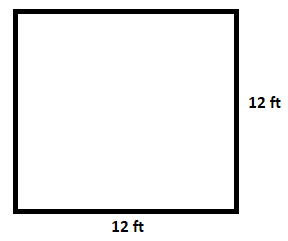
And therefore, the perimeter of the square is equal to $4a=4\times 12=48ft.$
Similarly, we can find the area of the given square.
As we know the area of the square with side $a$ units can be found by the formula ${{a}^{2}}.$
So, when we apply this formula to find the area of square with side $12ft.,$ we will get the area of the square as ${{12}^{2}}=144f{{t}^{2}}.$
Hence the perimeter of the given square is $48ft.$ and the area of the given square is $144f{{t}^{2}}.$

Note: We should always remember that a square is a rectangle with all the sides the same. So, as we know the perimeter of a rectangle can be found by the formula $2\times $(length $+$ breadth). And the area of a rectangle can be found by the formula length $\times $ breadth.