Question

$ P $ and $ Q $ are respectively the midpoint of sides $ AB $ and $ BC $ of a triangle $ ABC $ and $ R $ is the midpoint of $ AP $ , show that

I. $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ARC} \right) $
II. $ {\rm{ar}}\left( {RQC} \right) = \dfrac{3}{8}{\rm{ar}}\left( {ABC} \right) $
III. $ {\rm{ar}}\left( {PBQ} \right) = {\rm{ar}}\left( {ARC} \right) $

Answer 1

Hint: In the first proof since $ P $ is the midpoint of $ AB $ so $ {\rm{ar}}\left( {APC} \right) = {\rm{ar}}\left( {BPC} \right) $ . Get $ {\rm{ar}}\left( {PRQ} \right) $ in term of $ {\rm{ar}}\left( {ABC} \right) $ and $ {\rm{ar}}\left( {ARC} \right) $ in terms of $ {\rm{ar}}\left( {ABC} \right) $ . For the second proof take $ {\rm{ar}}\left( {RQC} \right) $ as sum of $ {\rm{ar}}\left( {PRQ} \right) $ and $ {\rm{ar}}\left( {BPQ} \right) $ . For the third proof write $ {\rm{ar}}\left( {PBQ} \right) $ in terms of $ {\rm{ar}}\left( {ABC} \right) $ and $ {\rm{ar}}\left( {ARC} \right) $ in terms of $ {\rm{ar}}\left( {ABC} \right) $ and then equate them.

Complete step-by-step answer:
 $ P $ and $ Q $ are respectively the midpoints of sides $ AB $ and $ BC $ of a triangle $ ABC $ and $ R $ is the midpoint of $ AP $ .

The following is the schematic diagram of the triangle ABC.

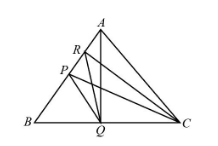
(i)
To prove that
 $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ARC} \right) $

We know that the area of triangles are equal that is $ {\rm{ar}}\left( {PRQ} \right) = {\rm{ar}}\left( {BPQ} \right) $ . This is because of the property of a median in which median divides it into two triangles of equal area.
Since, $ R $ is midpoint in line AP then form the property of median the area $ {\rm{ar}}\left( {ARQ} \right) $ is equal to half times $ {\rm{ar}}\left( {APQ} \right) $ .
Midpoint divides the triangles in two equal parts.
 $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABC} \right) $

To find the relation for $ {\rm{ar}}\left( {ARC} \right) $ , Since, we know that $ R $ is the midpoint of $ AP $ we have,
 $ {\rm{ar}}\left( {ARC} \right) = \dfrac{1}{2}{\rm{ar}}\left( {APC} \right) $ …….(1)
And it is known that $ P $ is the midpoint of $ AB $ we have,
 $ {\rm{ar}}\left( {APC} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABC} \right) $ ……(2)
On substituting the value from equation (2) in (1) we get,
 $ \begin{array}{c}
{\rm{ar}}\left( {ARC} \right) = \dfrac{1}{4}{\rm{ar}}\left( {ABC} \right)\\
\dfrac{1}{2} \times {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{4} \times {\rm{ar}}\left( {ARC} \right)
\end{array} $
On multiplying with $ 2 $ on both sides we get,
 $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2} \times {\rm{ar}}\left( {ARC} \right) $
Hence, it is proved that $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2} \times {\rm{ar}}\left( {ARC} \right) $ .

(ii)
To prove that
 $ {\rm{ar}}\left( {RQC} \right) = \dfrac{3}{8}{\rm{ar}}\left( {ABC} \right) $
We know that the area of triangles are equal that is $ {\rm{ar}}\left( {RQC} \right) = {\rm{ar}}\left( {RBQ} \right) $ . This is because of the property of a median in which median divides it into two triangles of equal area.
Also, medium of a $ A $ divides it into triangles of equal areas is equal to $ {\rm{ar}}\left( {PRQ} \right) + {\rm{ar}}\left( {BPQ} \right) $ .
Since, $ Q $ is the midpoint $ ABC $ so $ {\rm{ar}}\left( {ABQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {BPQ} \right) $ and since $ P $ is the midpoint of $ BPQ $ so $ {\rm{ar}}\left( {AQP} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABQ} \right) $ .
Also, $ R $ is the midpoint of $ ABQ $ so $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABC} \right) $ .
On combining all the equations, we have,
  $ {\rm{ar}}\left( {PRQ} \right) = \dfrac{1}{8}{\rm{ar}}\left( {ABC} \right) $
 $ \begin{array}{c}
{\rm{ar}}\left( {RQC} \right) = {\rm{ar}}\left( {PRQ} \right) + {\rm{ar}}\left( {BPQ} \right)\\
 = \dfrac{1}{8}{\rm{ar}}\left( {ABC} \right) + \dfrac{1}{2}{\rm{ar}}\left( {PBC} \right)\\
 = \dfrac{1}{8}{\rm{ar}}\left( {ABC} \right) + \dfrac{1}{4}{\rm{ar}}\left( {ABC} \right)\\
 = \dfrac{3}{8}{\rm{ar}}\left( {ABC} \right)
\end{array} $
Hence, proved that $ {\rm{ar}}\left( {RQC} \right) = \dfrac{3}{8}{\rm{ar}}\left( {ABC} \right) $ .

 (iii)
To prove that
 $ {\rm{ar}}\left( {PBQ} \right) = {\rm{ar}}\left( {ARC} \right) $

Since, $ Q $ is the midpoint of $ ABC $ , so we have,
 $ {\rm{ar}}\left( {ABQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABC} \right) $

Also, $ P $ is the midpoint of $ ABC $ , so we get,
 $ {\rm{ar}}\left( {PBQ} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABQ} \right) $
On equating the above equation, we get,
 $ {\rm{ar}}\left( {PBQ} \right) = \dfrac{1}{4}{\rm{ar}}\left( {ABC} \right) $ …….(3)
Since, we know $ P $ is the midpoint of $ ABC $ and $ R $ is the midpoint of $ APC $ , so we get,
  $ {\rm{ar}}\left( {APC} \right) = \dfrac{1}{2}{\rm{ar}}\left( {ABC} \right) $
 $ {\rm{ar}}\left( {ARC} \right) = \dfrac{1}{2}{\rm{ar}}\left( {APC} \right) $
Hence, on combining above both equations, we get,
 $ {\rm{ar}}\left( {ARC} \right) = \dfrac{1}{4}{\rm{ar}}\left( {ABC} \right) $ ……(4)
We will combine equations (3) and (4), we get,
 $ {\rm{ar}}\left( {PBQ} \right) = {\rm{ar}}\left( {ARC} \right) $

Note: Make sure that when the point is midpoint on a line then we can say that area can be divided into two equal parts. If it is not a mid-point area cannot be divided into two triangles with equal areas.