Question

One angle of a seven-sided polygon is 114 and each of the other six angles is \[x^{\circ}.\] The value of x is:
\[\left( a \right){{114}^{\circ}}\]
\[\left( b \right){{121}^{\circ}}\]
\[\left( c \right){{131}^{\circ}}\]
\[\left( d \right){{151}^{\circ}}\]

Answer 1

Hint: To solve this question, we will first calculate the sum of the interior angle by writing them as 6x + 114 as 6 angles are of measure x and one of 114. Then we will finally equate it to the formula of the sum of the interior angles of n sides polygon as \[\left( 2n-4 \right)\times 90\] to get the result.

Complete step-by-step solution
We are given that one angle of a seven-sided polygon is 114. A seven-sided polygon looks like the figure below.

The 7 sides are also mentioned in the figure given that each of the six angles is x degrees. Therefore, the angles are as:

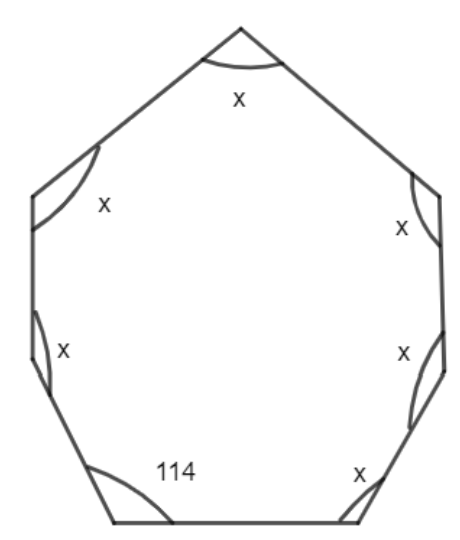
There is a formula of the sum of the interior angles of an n sided polygon given as \[\left( 2n-4 \right)\times 90....\left( i \right)\]
Now, the given one angle is 114. The other 6 sides measure x. Therefore, the sum of all interior angles is \[6x+114.....\left( ii \right)\]
Using the formula stated above in the equation (i) and equating to the equation (ii), we get,
\[6x+114=\left( 2n-4 \right)\times 90\]
Using n = 7, we have,
\[\Rightarrow 6x+114=\left( 2\times 7-4 \right)\times 90\]
Simplifying the bracket as 14 - 4 = 10 and taking 114 to the RHS, we have
\[\Rightarrow 6x=10\times 90-114\]
\[\Rightarrow 6x=900-114\]
\[\Rightarrow 6x=786\]
\[\Rightarrow x={{131}^{\circ }}\]
Therefore, the value of x is 131 degrees. Hence, the option (c) is the right answer.

Note: A possibility of mistake in this question is directly equating \[7{{x}^{\circ }}\] to \[\left( 2n-4 \right)\times {{90}^{\circ }}.\] This would be wrong as one measure of the angle is already given as \[{{114}^{\circ }}.\] We only need 6x and not 7x and hence \[6x+114=\left( 2n-4 \right)\times {{90}^{\circ }}\] and not the above written.