
What must be added to ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ . So that result is exactly divisible by ${{x}^{2}}+x-2$ ?
Answer
594k+ views
Hint: Divide the expression ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ by the term ${{x}^{2}}+x-2$ to get the quotient and remainder. Now, use the Euclid’s division lemma, given as
a = bq + r
where ‘a’ is divided by ‘b’ and quotient and remainder are denoted by q and r respectively. Try to observe the above relation as $a+\left( -r \right)=bq$ to get the result.
Complete step-by-step answer:
As, we know the Euclid’s division lemma is given as
a = bq + r……….(i)
where ‘a’ is the dividend, ‘b’ is divisor and q and r are quotient and remainder when ‘a’ is divided by ‘b’.
Now, we can rewrite the equation(i) as
a – r = bq
a + (-r) = bq ……..(ii)
So, we can observe that the dividend (a) will become multiple of divisor (b), if (-r) negative of the remainder is added to it i.e. a + (-r) will be divisible by b.
Now coming to question, we need to determine the term that should be added to ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ so that the result is divisible by ${{x}^{2}}+x+2$
So, let us divide the given expression by ${{x}^{2}}+x-2$ to get the remainder.
Hence, we can get the division of ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ by ${{x}^{2}}+x+2$ in following ways as
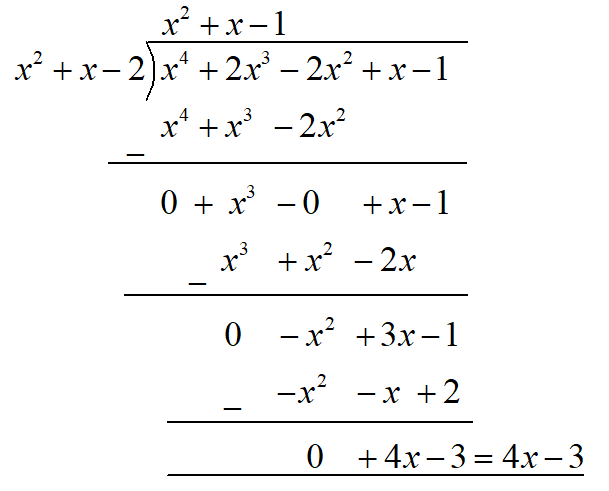
Now, we get the remainder by the division of the given expressions as $4x-3$
Hence, we need to add the negative of this remainder to the expression ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ to get divisible by expression ${{x}^{2}}+x-2$ , from the equation (ii).
So, we get negative of remainder as
$r=-\left( 4x-3 \right)=-4x+3$
Hence, we need to add this term to the expression ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ .So, we get the result as
$\begin{align}
& ={{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1-4x+3 \\
& ={{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}-3x+2 \\
\end{align}$
Hence, the result ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}-3x+2$ will be divisible by ${{x}^{2}}+x-2$
Note: One may go wrong if he/she adds the remainder to the dividend $\left( {{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1 \right)$ to get an expression which will be divisible by ${{x}^{2}}+x-2$ . So, always solve these questions by fundamental rules. Any dividend will be divisible by divisor, if remainder is subtracted from dividend. So, always take care of it for future reference as well.
One may go wrong with the division step as well. So, taking care while dividing the expression by the given term is the key point of the question as well.
Don’t confuse with the Euclid’s division lemma, it is a simple expression of the division law, given as
Dividend = Divisor x Quotient + Remainder.
a = bq + r
where ‘a’ is divided by ‘b’ and quotient and remainder are denoted by q and r respectively. Try to observe the above relation as $a+\left( -r \right)=bq$ to get the result.
Complete step-by-step answer:
As, we know the Euclid’s division lemma is given as
a = bq + r……….(i)
where ‘a’ is the dividend, ‘b’ is divisor and q and r are quotient and remainder when ‘a’ is divided by ‘b’.
Now, we can rewrite the equation(i) as
a – r = bq
a + (-r) = bq ……..(ii)
So, we can observe that the dividend (a) will become multiple of divisor (b), if (-r) negative of the remainder is added to it i.e. a + (-r) will be divisible by b.
Now coming to question, we need to determine the term that should be added to ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ so that the result is divisible by ${{x}^{2}}+x+2$
So, let us divide the given expression by ${{x}^{2}}+x-2$ to get the remainder.
Hence, we can get the division of ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ by ${{x}^{2}}+x+2$ in following ways as
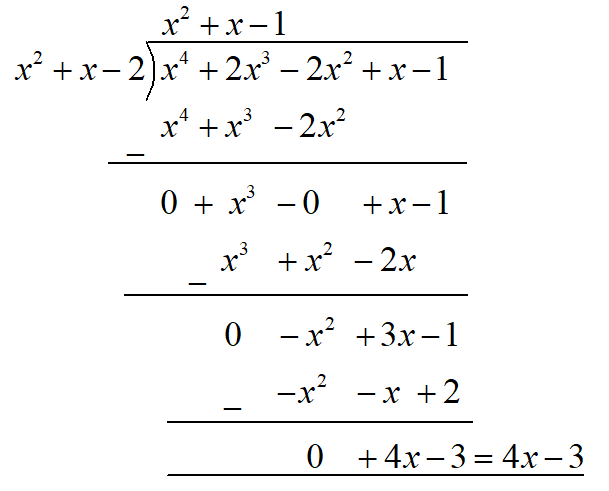
Now, we get the remainder by the division of the given expressions as $4x-3$
Hence, we need to add the negative of this remainder to the expression ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ to get divisible by expression ${{x}^{2}}+x-2$ , from the equation (ii).
So, we get negative of remainder as
$r=-\left( 4x-3 \right)=-4x+3$
Hence, we need to add this term to the expression ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1$ .So, we get the result as
$\begin{align}
& ={{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1-4x+3 \\
& ={{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}-3x+2 \\
\end{align}$
Hence, the result ${{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}-3x+2$ will be divisible by ${{x}^{2}}+x-2$
Note: One may go wrong if he/she adds the remainder to the dividend $\left( {{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}+x-1 \right)$ to get an expression which will be divisible by ${{x}^{2}}+x-2$ . So, always solve these questions by fundamental rules. Any dividend will be divisible by divisor, if remainder is subtracted from dividend. So, always take care of it for future reference as well.
One may go wrong with the division step as well. So, taking care while dividing the expression by the given term is the key point of the question as well.
Don’t confuse with the Euclid’s division lemma, it is a simple expression of the division law, given as
Dividend = Divisor x Quotient + Remainder.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




