Question

What is the minimum value of the refractive index for the $ {45^ \circ } $ prism which is used to turn a beam of light by total internal reflection through a right angle?
 $ (i){\text{ 1}}{\text{.67}} $
 $ (ii){\text{ 1}}{\text{.5}} $
 $ (iii){\text{ 1}}{\text{.41}} $
 $ (iv){\text{ 2}}{\text{.0}} $

Answer 1

Hint: When the ray of light enters into a prism then it gets totally internally reflected for a certain value of refractive of the prism for a given angle of prism. The ray of light will get totally internally reflected when it hits the surface of the prism at the right angle. We will find the value of the refractive index for which it gets totally internally reflected.
 $ {\mu _1}{\text{ }} \times {\text{ sin}}{\theta _1}{\text{ = }}{\mu _2}{\text{ }} \times {\text{ sin}}{\theta _2} $ .

Complete answer:
Let a ray of light travels from refractive index $ {\mu _1} $ and enter into a prism whose refractive is $ {\mu _2} $ , then it will suffer the total internal reflection when the angle of reflection is a right angle which means that $ {\theta _2} $ will be right angle according to question.

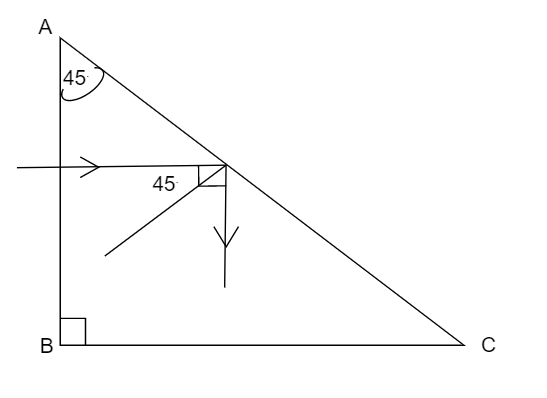
Assuming that the ray of light travels from air whose refractive index is equal to one. Therefore the value of $ {\mu _1} $ will be equal to one. Also the angle of incident is $ {45^ \circ } $ . Therefore on substituting the values we get result as,
 $ {\mu _1}{\text{ }} \times {\text{ sin}}{\theta _1}{\text{ = }}{\mu _2}{\text{ }} \times {\text{ sin}}{\theta _2} $
 $ {\mu _1}{\text{ }} \times {\text{ sin(4}}{{\text{5}}^ \circ }{\text{) = }}{\mu _2}{\text{ }} \times {\text{ sin(9}}{{\text{0}}^ \circ }{\text{)}} $
 $ \mu {\text{ = }}\dfrac{1}{{\sin ({{45}^ \circ })}} $
We know that $ \sin ({45^ \circ }){\text{ = }}\dfrac{{\text{1}}}{{\sqrt 2 }} $ , thus substitute the value,
 $ \mu {\text{ = }}\dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}} $
 $ \mu {\text{ = }}\sqrt 2 $
 $ \mu {\text{ = 1}}{\text{.41}} $
 Thus the minimum value of the refractive index for total internal reflection must be minimum $ 1.41 $ .

Note:
We can also find the value of refractive for angle of prism by using formula $\mu= \dfrac{1}{\sin A}$, where A is the angle of prism. But the result from both cases will be equal to $ 1.41 $ .
We have used the refractive index of air as one which must be remembered for solving such problems. Total internal reflection is commonly written as TIR. Due to this effect the light gets trapped inside the prism which is the cause of the brightness of the prism.