Question

Prove that a parallelogram circumscribing a circle is a rhombus.

Answer 1

Hint: Use the property that tangents from an external point to a circle are equal in length. Hence show that all the sides of the parallelogram are equal.A quadrilateral (parallelogram) in which all four sides have equal in length then it is said to be rhombus.Finally show that the parallelogram is a rhombus.

Complete step-by-step answer:
Given: A parallelogram ABCD circumscribing a circle.
To prove: ABCD is a rhombus

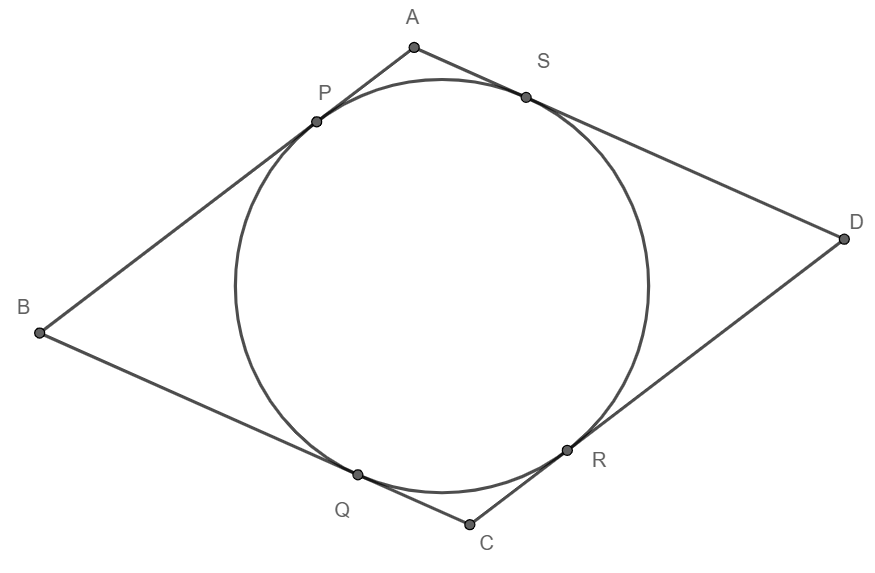
Proof:
We know that tangents drawn from an external point to a circle are equal in length.
We have B is an external point, and BP and BQ are tangents to the circle. So, we have
BP = BQ.
Similarly, C is an external point, and CQ and CR are external tangents.
Hence CQ = CR.
Similarly DR = DS and AS = AP
We have
AP = AS
Adding BP on both sides, we get
AP+BP = AS+BP
But BP = BQ and AP+BP = AB, so we have
AB = AS+ BQ
Adding CQ on both sides, we get
AB + CQ = AS+ BQ +CQ
But CQ = CR and BQ +CQ = BC, so we have
AB + CR = AS + BC
Adding DR on both sides, we get
AB + CR + DR = AS + BC + DR.
But DR = DS and CR + CR = CD, so we have
AB + CD = AS+DS + BC
But, AS + DS = AD, so we have
AB + CD = AD + BC.
Since ABCD is a parallelogram, we have AB = CD and AD = BC (Because opposite sides of a parallelogram are equal).
Hence, we have AB + AB = AD +AD
i.e 2AB = 2AD
Hence AB = AD.
But AB = CD and AD = BC
Hence AB = BC = CD = DA
Hence ABCD is a rhombus.

Note: [1] A quadrilateral in which all four sides have equal in length then it is said to be rhombus.
[2] Lengths of tangents from an external point are equal. This can be shown by joining the point to the centre of the circle and connecting points of contact to the centre. Hence show that the two triangles so formed are congruent.
[3] The circle which is circumscribed by the rhombus is called the incircle of the rhombus.