Question

Minimise and maximise $z = 600x + 400y$
Subject to the following conditions:
$x + 2y \leqslant 12$
$2x + y \leqslant 12$
$4x + 5y \leqslant 20$
$x \geqslant 0,y \geqslant 0$ by the graphical method

Answer 1

Hint: First draw the graph and find out the intersection point of every intersecting line for example $x \geqslant 0,y \geqslant 0$
It represents that it will lie in the first quadrant and then draw the graph of $x + 2y = 12$ and $2x + y = 12$, $4x + 5y = 20$ then find out the intersection point, then put that point in $z = 600x + 400y$ and then find out the maxima and minima of the following

Complete step-by-step answer:
Here we need to minimise and maximise $z = 600x + 400y$
Which is subjected to the following conditions:
$x + 2y \leqslant 12$
$2x + y \leqslant 12$
$4x + 5y \leqslant 20$
$x \geqslant 0,y \geqslant 0$ by the graphical method
So their graph represents the first quadrant as every point in the first quadrant satisfies$x \geqslant 0,y \geqslant 0$
(2) Now let us draw the graph of $x + 2y = 12$
So for $x = 0$, $0 + 2y = 12$
$ \Rightarrow $$y = 6 \Rightarrow (0,6)$
For$y = 0$, $x + 0 = 12$
$ \Rightarrow $$x = 12 \Rightarrow (12,0)$
(3) Now if we draw the graph of $2x + y = 12$
So for the graph we need two points
So for$x = 0$, $0 + y = 12$
$ \Rightarrow $$y = 12 \Rightarrow (0,12)$
For$y = 0$, $2x + 0 = 12$
$ \Rightarrow $$x = 6 \Rightarrow (6,0)$
So with the point $(0,12),(6,0)$ we can draw the line
Let $C$ be $(0,12)$ and $D$ be $(6,0)$
(3) Now for$4x + 5y \leqslant 20$, we need to draw the graph of $4x + 5y = 20$
So for $x = 0$, $0 + 5y = 20$
$ \Rightarrow $$y = 4 \Rightarrow (0,4)$
So let this point be $E(0,4)$
For $y = 0$, $4x + 0 = 20$
$ \Rightarrow $$x = 5 \Rightarrow (5,0)$
So let this point be $F(5,0)$
So $(0,4),(5,0)$ are the coordinate axes.
Now if we draw every graph in one graph, we will get

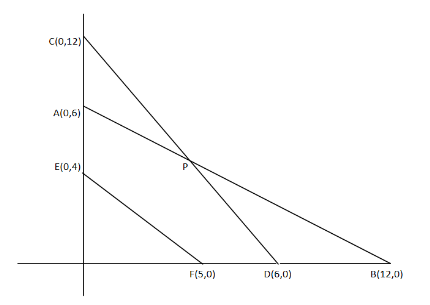
So we need to find the point P which is formed by the intersection of the line $AB,CD$
$ \Rightarrow $$AB = x + 2y = 12$
$ \Rightarrow $$x = 12 - 2y$
$ \Rightarrow $$CD = 2x + y = 12$
Put $x = 12 - 2y$ in $CD$
$ \Rightarrow $$2(12 - 2y) + y = 12$
$ \Rightarrow $$3y = 12$
$ \Rightarrow $$y = 4$
$ \Rightarrow $$x = 12 - 2(4) = 4$
So we get the point P
Now as we know $z = 600x + 400y$
Now the common shaded region of the curve will be

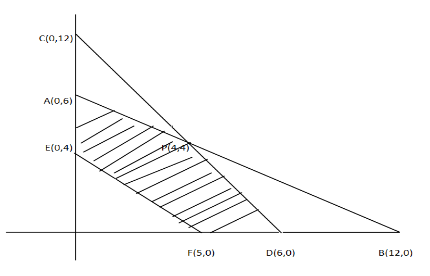
Now for the point A$(0,6)$
$ \Rightarrow $$z = 600x + 400y$
$ \Rightarrow $$z = 600(0) + 400(6)$
   $ = 2400$
For the point E $(0,4)$
$ \Rightarrow $$z = 600x + 400y$
$ \Rightarrow $$z = 600(0) + 400(4)$
    $ = 1600$
For the point F $(5,0)$
$ \Rightarrow $$z = 600x + 400y$
$ \Rightarrow $$z = 600(5) + 400(0)$
    $ = 3000$
For the point D $(6,0)$
$ \Rightarrow $$z = 600x + 400y$
$ \Rightarrow $$z = 600(6) + 400(0)$
   $ = 3600$
For the point P $(4,4)$
$ \Rightarrow $$z = 600x + 400y$
$ \Rightarrow $$z = 600(4) + 400(4)$
    $ = 4000$
So the maximum value of $z$ is at P$ = 4000$
Minimum value of $z$ is at E$ = 1600$

Note: To draw a graph of this line, we must at least need two points or one point and one slope.
If the two points are $({x_1},{y_1}),({x_2},{y_2})$ then the equation of the line is given by
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$
Or if we are given the slope $m$ of the line $AB$ passing from the point $A({x_1},{y_1})$ then the equation is given by $y - {y_1} = m(x - {x_1})$
General formula for the straight line is
$y = mx + c$