Question

What do you mean by eccentricity? Explain.

Answer 1

Hint: Eccentricity is the measure of how circular a curve is. Eccentricity is different for different conic sections and constant for that particular conic section. The eccentricity of the ellipse is (e < 1), eccentricity of the circle is (e = 0), eccentricity of parabola is (e = 1), eccentricity of hyperbola is (e > 1). Eccentricity is also defined by how much the conic section deviates from being circular.

Complete step-by-step answer:
The eccentricity in the conic section uniquely characterises the shape where it should possess a non- negative real number.
 In general, eccentricity means a measure of how much the deviation of the curve has occurred from the circularity of the given shape.
We know that the section obtained after the intersection of a plane with the cone is called the conic section. We will get different kinds of conic sections depending on the position of the intersection of the plane with respect to the plane and the angle made by the vertical axis of the cone.
We know that there are different conics such as a parabola, ellipse, hyperbola and circle. The eccentricity of the conic section is defined as the distance from any point to its focus, divided by the perpendicular distance from that point to its nearest directrix. The eccentricity value is constant for any conics.
Eccentricity is denoted by the small letter “e”.
$\text{Eccentricity}\,\,\text{= }\dfrac{\text{c}}{\text{a}}$
Where,
c = distance from the centre of the focus to vertex
a = semi-major axis
Let's understand with the example of an ellipse.

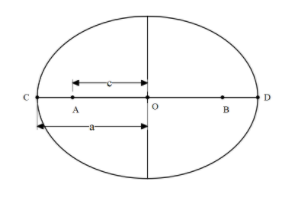
The above diagram shows the figure of an ellipse, with O is the vertex and A, B are the two foci of the ellipse.
OD is the semi major axis of the ellipse.
The ratio of the $\dfrac{c}{a}$ gives the eccentricity of the ellipse.
The eccentricity of the ellipse less than one $\left( e<1 \right)$ .
A circle is the special case of an ellipse where $\left( e=0 \right)$ .


Note: It is easily confused between the semi major axis and the semi-minor axis. One trick to remember in case of an ellipse is to calculate the length from the centre to the most elongated part that gives the semi-major axis of the ellipse. One note needs to be considered that the distance from both the foci to the vertex is the same.