Question

What is the maximum possible radius of a circle that can be fitted inside a square of side ‘a’ unit.
(a) \[\dfrac{a}{2}\]
(b) \[\dfrac{a}{3}\]
(c) \[\dfrac{a}{4}\]
(d) \[\dfrac{a}{5}\]

Answer 1

Hint: This question belongs to the topic geometry, in this question we do not have to give the steps of construction, but just give the justification about the maximum possible radius of a circle that can be fitted inside a square whose length of side is ‘a’ unit. So, in order to solve this question, first of all we need a diagram to see and measure the maximum possible radius of the circle. Then we need to understand the radius and diameter, and their relation. Then, finally we can answer this question.

Complete step-by-step answer:
Now, if we want to solve and answer this question, then we need to have a diagram of this question, for our understanding.
So, the diagram related to this question is given below,

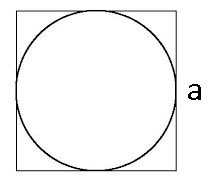
Here, we can see the biggest circle which can be fitted inside a square of side ‘a’ unit. If we increase the radius of the circle, then the circle will come out of the square and it will be no more fitted in the square.
In a circle, the biggest line segment which can be measured is known as diameter.
We know that Diameter is the length of the line through the center that touches two points on the edge of the circle.
In the diagram, we can see that the diameter of the circle will be equal to ‘a’ unit.
Hence, diameter \[=a\]
As we know, there is a relation between diameter and radius.
The relation is,
\[\text{diameter}=2\times (\text{radius})\]
If we put the value of diameter in this relation, we can find the radius of the circle.
After putting the value of diameter in the relation, we get,
\[\begin{align}
  &\Rightarrow \text{diameter}=2\times (\text{radius}) \\
 &\Rightarrow a=2\times (radius) \\
 &\Rightarrow radius=\dfrac{a}{2} \\
\end{align}\]
Hence, we can say that the maximum radius of a circle which can be fitted in the square of side ‘a’ unit is \[\dfrac{a}{2}\].

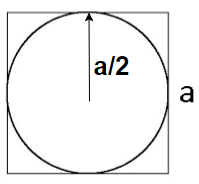
Note: In this question, the chances of error is that every student has its own opinion, so if anyone got confused and drawn a square of side ‘a’ unit inside a circle, instead of a circle inside a square of side ‘a’ unit and starts finding the radius, then the solution will become wrong. Also, remember the relation between radius and diameter as it is also a main part of the solution.