Question

$[{M^{ - 1}}{L^3}{T^{ - 2}}]$ are the dimensions of:
A. Acceleration due to gravity
B. Gravitational constant
C. Gravitational force
D. Gravitational potential energy

Answer 1

Hint There is a very simple way to solve these types of questions. Consider each option separately and write their formula. Now replace all the masses with $M$, all the lengths or distances with $L$ and all the times with $T$. Solve it and you will get the result.

 Complete step-by-step solution:For option B: Gravitational constant
Formula for gravitational constant is
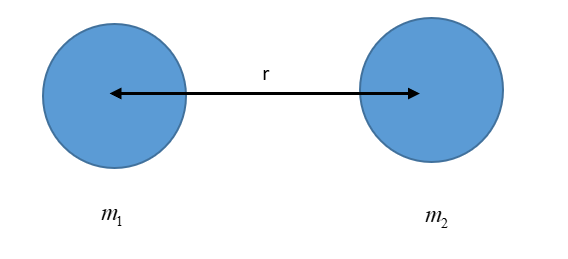
 $G = \dfrac{{F{r^2}}}{{{m_1}{m_2}}}$---(1)
Where $F = $Force exerted between two bodies
$R = $distance between centre of two bodies
${m_1},{m_2}$Are masses of the bodies.

$F = ma$
$a = \dfrac{v}{t} = \dfrac{s}{{{t^2}}}$
To write dimensional formula, replace all masses with “$M$”, replace all the lengths and distances with “$L$” and all the times with “$T$”.
So dimensional formula of force will be $[{M^1}{l^1}{t^{ - 2}}]$
Dimensional formula for ${r^2}$will be $[{M^0}{L^2}{T^0}]$
Dimensional formula of m1m2 will be$[{M^2}{L^0}{T^0}]$
Now putting these 3 in equation 1, we get:
$
  G = [{M^1}{L^1}{T^{ - 2}}] \times [{M^0}{L^2}{T^0}]/[{M^2}{L^0}{T^0}] \\
  G = [{M^1}{L^1}{T^{ - 2}}] \times [{L^2}]/[{M^2}] \\
 $
Take all the denominator values in numerator, we get:
$G = [{M^1}{L^1}{T^{ - 2}}] \times [{L^2}] \times [{M^{ - 2}}]$
Adding up all the powers we get:
$G = [{M^{ - 1}}{L^3}{T^{ - 2}}]$

Note:- Make sure, while expanding the formula, and expand it to its simplest form and try to for every term in the formula try to write all in terms of$M,L,T$. And make sure while taking the denominator to the numerator change the power from positive to negative of only the denominator variables.