Question

What is the limit as x approaches infinity of \[{{e}^{x}}\]?

Answer 1

Hint: In this type of question we have to use the concept of limit at infinity. We know that the idea of a limit is the basis of all calculus. Also we know that, a limit tells us the value that the given function approaches as that function’s input approaches to some number.

Complete step by step answer:
In the given question, we have to find the limit of \[{{e}^{x}}\] as \[x\] approaches to \[\infty \].
Hence, the function is \[f\left( x \right)={{e}^{x}}\] and limit as \[x\] approaches to \[\infty \] i.e. \[x \to \infty \]
\[\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\displaystyle \lim_{x \to \infty }{{e}^{x}}\]
By applying the value of \[x\] as \[\infty \], we can write,
\[\Rightarrow \displaystyle \lim_{x \to \infty }{{e}^{x}}={{e}^{\infty }}\]
As we know that, the domain of \[{{e}^{x}}\] is the whole of \[\mathbb{R}\] and the range is \[\left( 0,\infty \right)\]. Also \[{{e}^{x}}\] is continuous function defined on the whole of \[\mathbb{R}\] and infinitely differentiable, with \[\dfrac{d}{dx}{{e}^{x}}={{e}^{x}}\].
Hence, the value of \[{{e}^{\infty }}=\infty \]
\[\Rightarrow \displaystyle \lim_{x \to \infty }{{e}^{x}}=\infty \]
Thus, the limit as \[x\] approaches \[\infty \] of \[{{e}^{x}}\] is \[\infty \].

Note: In this type of question one of the students may state the result with the help of a graph also. The function \[f\left( x \right)={{e}^{x}}\] is an equation in which the variable is an exponent, and the graph is exponentially increasing with respect to \[x\]. Where, \[x\] is a real number and \[e\] is a positive constant. The graph for \[f\left( x \right)={{e}^{x}}\] is as follows:

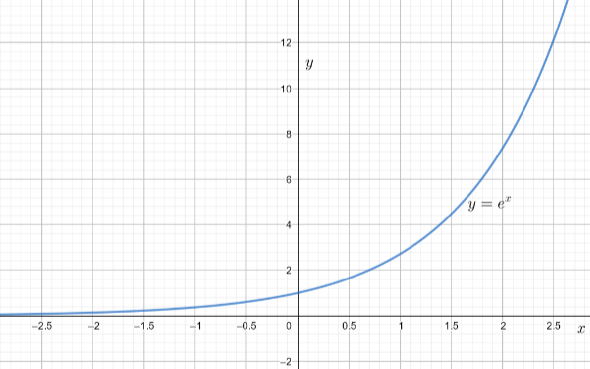
From the above graph of \[{{e}^{x}}\] with respect to \[x\] we can clearly observe that as \[x\] approaches to \[\infty \], the function \[{{e}^{x}}\] also approaches to \[\infty \].
Thus, the limit as \[x\] approaches \[\infty \] of \[{{e}^{x}}\] is \[\infty \].