
Let ABC be a triangle such that $\angle ACB = \dfrac{\pi }{6}$ and let a, b and c denote the length of the sides opposite to A, B and C respectively. The value(s) of x for which $a = {x^2} + x + 1$, $b = {x^2} - 1$ and $c = 2x + 1$ is(are)
A. $ - \left( {2 + \sqrt 3 } \right)$
B. $1 + \sqrt 3 $
C. $2 + \sqrt 3 $
D. $4\sqrt 3 $
Answer
591k+ views
Hint: To solve this question, we will use the concept of Cosine rule (the law of Cosine). According to the Cosine rule, the square of the length of any side of a triangle equals to the sum of the squares of the length of the other sides minus twice of their product multiplied by the cosine of their included angle, i.e. ${a^2} = {b^2} + {c^2} - 2bc\cos A$, ${b^2} = {a^2} + {c^2} - 2ac\cos B$ and ${c^2} = {a^2} + {b^2} - 2ab\cos C$
Complete step-by-step answer:
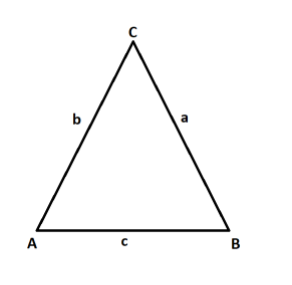
Given that,
ABC is a triangle and $\angle ACB = \dfrac{\pi }{6}$
a = length of side opposite to A.
b = length of side opposite to B.
c = length of side opposite to C.
we have to find out the value of x, when $a = {x^2} + x + 1$, $b = {x^2} - 1$ and $c = 2x + 1$
So,
As we know that,
According to the Cosine rule, the square of the length of any side of a triangle equals to the sum of the squares of the length of the other sides minus twice their product multiplied by the cosine of their included angle.
We have given,
$\angle ACB = \dfrac{\pi }{6}$
Therefore, applying the Cosine rule for $\angle C$,
${c^2} = {a^2} + {b^2} - 2ab\cos C$
This can also be written as:
$\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Putting the value of a, b and c in the above equation, we will get
$\cos \dfrac{\pi }{6} = \dfrac{{{{\left( {{x^2} + x + 1} \right)}^2} + {{\left( {{x^2} - 1} \right)}^2} - {{\left( {2x + 1} \right)}^2}}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}$
By using the appropriate identities, we will solve this
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^4} + 2{x^3} - 3{x^2} - 2x + 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}\]
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)\left( {{x^2} - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}\]
Dividing \[\left( {{x^2} - 1} \right)\] from numerator and denominator, we will get
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)}}\]
\[ \Rightarrow \sqrt 3 = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)}}\]
Now taking \[\left( {{x^2} + x + 1} \right)\] to the left side,
\[ \Rightarrow \sqrt 3 \left( {{x^2} + x + 1} \right) = \left( {2{x^2} + 2x - 1} \right)\]
Simplifying this,
\[ \Rightarrow {x^2}\left( {\sqrt 3 - 2} \right) + x\left( {\sqrt 3 - 2} \right) + \left( {\sqrt 3 + 1} \right) = 0\] ……… (i)
Now, we find out the roots of the above quadratic equation using the formula,
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ ……… (ii)
Comparing equation (i) with $a{x^2} + bx + c = 0$, we will get
$a = b = \sqrt 3 - 2$ and $c = \sqrt 3 + 1$
Putting these values in equation (ii),
\[
\Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2} - 4\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 + 1} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 - 2 - 4\sqrt 3 - 4} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\Rightarrow x = \dfrac{{\left( {2 - \sqrt 3 } \right) \pm \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\]
Now, we get 2 values of x,
\[x = \dfrac{{\left( {2 - \sqrt 3 } \right) + \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}}\],
Rationalising it,
\[
x = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\
x = - \left( {\sqrt 3 + 2} \right) \\
\]
Or,
\[x = \dfrac{{\left( {2 - \sqrt 3 } \right) - \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}}\],
Rationalising it,
\[
x = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\
x = \left( {1 + \sqrt 3 } \right) \\
\]
Hence, the value of x will be \[\left( {1 + \sqrt 3 } \right)\] as x > 0.
Therefore, the correct answer is option (B).
Note: Whenever we ask such questions, we have to remember that Cosine rule will be used when two sides and included angles are given or when three sides of a triangle is given. The sine rule states that the sides of a triangle are proportional to the sines of the opposite angles, i.e. given as: $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$
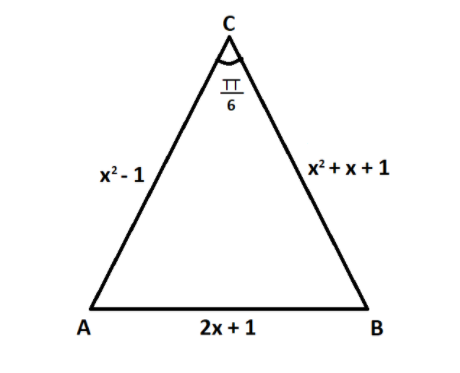
Complete step-by-step answer:

Given that,
ABC is a triangle and $\angle ACB = \dfrac{\pi }{6}$
a = length of side opposite to A.
b = length of side opposite to B.
c = length of side opposite to C.
we have to find out the value of x, when $a = {x^2} + x + 1$, $b = {x^2} - 1$ and $c = 2x + 1$
So,
As we know that,
According to the Cosine rule, the square of the length of any side of a triangle equals to the sum of the squares of the length of the other sides minus twice their product multiplied by the cosine of their included angle.
We have given,
$\angle ACB = \dfrac{\pi }{6}$
Therefore, applying the Cosine rule for $\angle C$,
${c^2} = {a^2} + {b^2} - 2ab\cos C$
This can also be written as:
$\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Putting the value of a, b and c in the above equation, we will get
$\cos \dfrac{\pi }{6} = \dfrac{{{{\left( {{x^2} + x + 1} \right)}^2} + {{\left( {{x^2} - 1} \right)}^2} - {{\left( {2x + 1} \right)}^2}}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}$
By using the appropriate identities, we will solve this
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^4} + 2{x^3} - 3{x^2} - 2x + 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}\]
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)\left( {{x^2} - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)\left( {{x^2} - 1} \right)}}\]
Dividing \[\left( {{x^2} - 1} \right)\] from numerator and denominator, we will get
\[ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{2\left( {{x^2} + x + 1} \right)}}\]
\[ \Rightarrow \sqrt 3 = \dfrac{{\left( {2{x^2} + 2x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)}}\]
Now taking \[\left( {{x^2} + x + 1} \right)\] to the left side,
\[ \Rightarrow \sqrt 3 \left( {{x^2} + x + 1} \right) = \left( {2{x^2} + 2x - 1} \right)\]
Simplifying this,
\[ \Rightarrow {x^2}\left( {\sqrt 3 - 2} \right) + x\left( {\sqrt 3 - 2} \right) + \left( {\sqrt 3 + 1} \right) = 0\] ……… (i)
Now, we find out the roots of the above quadratic equation using the formula,
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ ……… (ii)
Comparing equation (i) with $a{x^2} + bx + c = 0$, we will get
$a = b = \sqrt 3 - 2$ and $c = \sqrt 3 + 1$
Putting these values in equation (ii),
\[
\Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2} - 4\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 + 1} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\Rightarrow x = \dfrac{{ - \left( {\sqrt 3 - 2} \right) \pm \sqrt {\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 - 2 - 4\sqrt 3 - 4} \right)} }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\Rightarrow x = \dfrac{{\left( {2 - \sqrt 3 } \right) \pm \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} \\
\]
Now, we get 2 values of x,
\[x = \dfrac{{\left( {2 - \sqrt 3 } \right) + \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}}\],
Rationalising it,
\[
x = \dfrac{1}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\
x = - \left( {\sqrt 3 + 2} \right) \\
\]
Or,
\[x = \dfrac{{\left( {2 - \sqrt 3 } \right) - \sqrt 3 }}{{2\left( {\sqrt 3 - 2} \right)}} = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}}\],
Rationalising it,
\[
x = \dfrac{{\left( {1 - \sqrt 3 } \right)}}{{\left( {\sqrt 3 - 2} \right)}} \times \dfrac{{\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)}} \\
x = \left( {1 + \sqrt 3 } \right) \\
\]
Hence, the value of x will be \[\left( {1 + \sqrt 3 } \right)\] as x > 0.
Therefore, the correct answer is option (B).
Note: Whenever we ask such questions, we have to remember that Cosine rule will be used when two sides and included angles are given or when three sides of a triangle is given. The sine rule states that the sides of a triangle are proportional to the sines of the opposite angles, i.e. given as: $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$

Recently Updated Pages
Complete reduction of benzene diazonium chloride with class 12 chemistry CBSE

How can you identify optical isomers class 12 chemistry CBSE

The coating formed on the metals such as iron silver class 12 chemistry CBSE

Metals are refined by using different methods Which class 12 chemistry CBSE

What do you understand by denaturation of proteins class 12 chemistry CBSE

Assertion Nitrobenzene is used as a solvent in FriedelCrafts class 12 chemistry CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

RNA and DNA are chiral molecules their chirality is class 12 chemistry CBSE

RNA and DNA are chiral molecules their chirality is class 12 chemistry CBSE

India is a sovereign socialist secular democratic republic class 12 social science CBSE

The correct structure of ethylenediaminetetraacetic class 12 chemistry CBSE

How many states of matter are there in total class 12 chemistry CBSE




