Question

Is the sum of any two sides of a triangle greater than the third side?

Answer 1

Hint: To answer this question, one should know the basics of triangles and its properties. We first try to use the basics of construction and then use results subsequently obtained to find the correct answer.

Complete step-by-step answer:

Before solving, we will first start with drawing a triangle ABC and introducing a few constructions that have to be made in order to arrive at the desired answer. We have a triangle as shown below. On this we will construct AD = AC. (as shown in the second figure which is below the first figure)

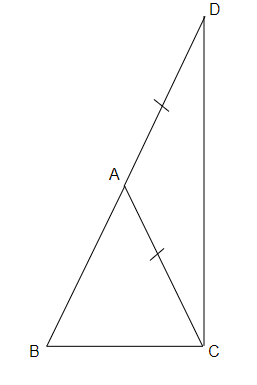
Now, that we are done with the necessary constructions, we are ready to solve the problem (we will only refer to the second figure from now on). We know that angles opposite to equal sides are always equal, thus in triangle ADC, we have,
Angle ADC = Angle ACD -- (1)
Also, side BD > AC (BD = AB + AD, now, since AC=AD, BD = AB + AC, thus BD > AC)
Thus, angle BCD > angle BDC (side opposite to the greater angle is longer)
Further, for triangle BDC, angle BDC is opposite to BC and angle BCD is opposite to BD. Thus, using the converse of the statement that side opposite to the greater angle is longer (since, angle BCD > angle BDC), we have,
BD > BC
AB+AD > BC
Since, AD = AC (by construction), we have,
AB + AC > BC
Hence, the sum of two sides of a triangle is always greater than the third side.
Hence, it is true.

Note: We should know that not only should the sum of two sides of a triangle be always greater than the third side, they can also never be equal to the third side. If the sum of the two sides of a triangle is equal to the third side, then a straight line is formed.