Question

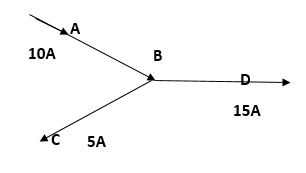
Is the following circuit correctly drawn?

A. Yes
B. No
C. Cannot be predicted
D. Insufficient data to reply

Answer 1

Hint: Kirchhoff’s first law states that the algebraic sum of all the currents at a junction should be zero or the current entering at a junction must be equal to current leaving at that junction. So apply Kirchhoff’s first law at the junction to see whether it satisfies or not.

Complete step by step answer:
Kirchhoff gave two laws to solve the meshed network. The first law states that the algebraic sum of all the currents at a junction must be zero. The sign convention here taken is that the current entering the junction should be taken as positive and the current leaving the circuit is taken to be negative. Or it can also be stated as the algebraic sum of all the currents entering a junction must be equal to the currents leaving the junction.
So if we apply the Kirchhoff’s current law at point B we see. The current entering the circuit is $10A$ and the current leaving the circuit is $15A+5A=20A$. So Kirchhoff’s law does not hold good at point B so the circuit is not drawn correctly.
So the correct option is B.
Additional Information: According to Kirchhoff’s second law around any closed loop or network, the algebraic sum of the changes in potential must be zero. Or the algebraic sum of the emfs in a closed loop of a circuit is equal to the sum of products of currents and resistance.
Applying Kirchhoff’s voltage law to a meshed network.
(i) We can take any direction, clockwise or anti-clockwise as the direction of the loop.
(ii) The emf of the cell is taken as positive if the direction of the loop is from its negative to positive terminal of the battery.

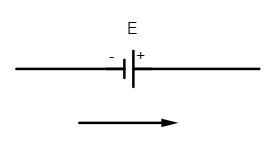
Here if the emf of cell is E then the potential across the cell is $V=+E$ (positive emf)
(iii) The emf of the cell is taken as negative if the direction of the loop is from its positive to negative terminal of the battery.

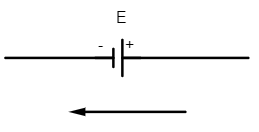
Here if the emf of cell is E then the potential across the cell is $V=-E$ (negative emf)

(iv) The current-resistance $\left( IR \right)$ product is taken as positive if the resistance is travelled in the same direction as the assumed loop.

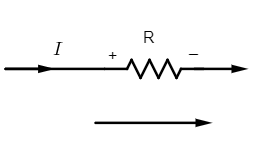
Here potential drop across the resistance R is $V=+IR$ (positive potential drop)
(v) The current-resistance $\left( IR \right)$ product is taken as negative if the resistance is travelled in the opposite direction as that of the assumed loop.

Here potential drop across the resistance R is $V=-IR$ (negative potential drop)

Note:
The Kirchhoff’s current law is based upon the conservation of charge. Kirchhoff's second law or Kirchhoff’s voltage law is based on the principle of conservation of energy. This is because of the conservative nature of electrostatic force. As the electrostatic force is conservative the total work done by it along any closed path must be zero.