Question

Inside a uniform spherical shell
(This question has Multiple correct answers)
A. The gravitational potential is zero.
B. The gravitational field is zero.
C. The gravitational potential is the same everywhere.
D. The gravitational field is the same everywhere.

Answer 1

Hint: A uniform spherical shell has a constant surface mass density. We should take a point inside the spherical shell of radius R centered at O. Then find the potential at that particular point P. We can do this by taking a small cross-section of the spherical shell, finding the corresponding potential at point P due to that cross-section and finally integrate over the whole spherical shell to get the total potential at point P.

Formula Used:
The gravitational potential(V) of a mass M at a distance R away from it, is given by
$V=-\dfrac{GM}{R}$

Complete step-by-step answer:

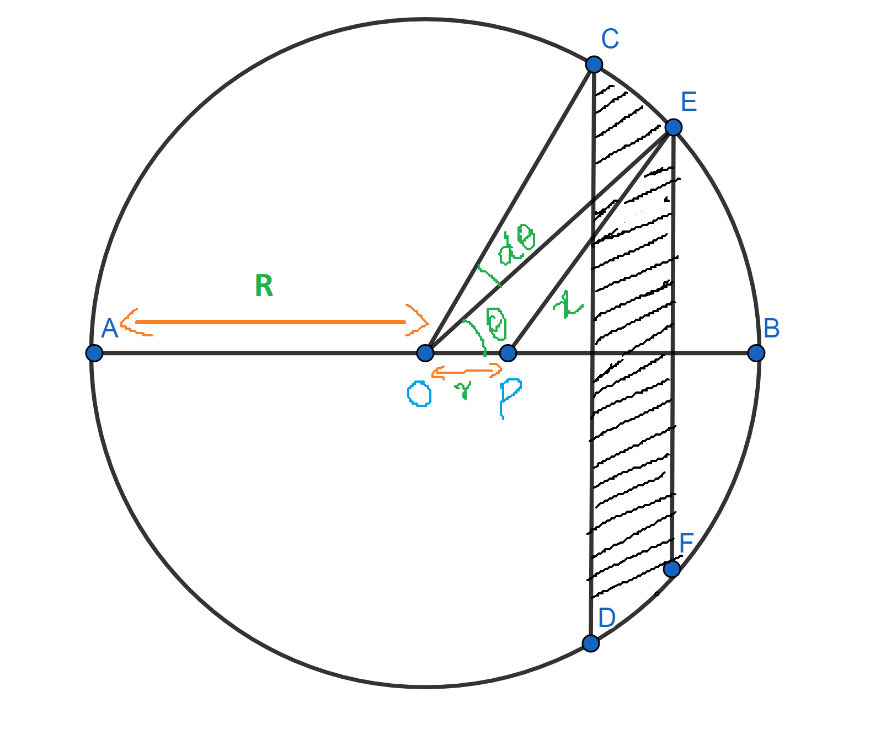
We will consider a spherical shell of radius R, having a constant surface mass density $\text{ }\!\!\sigma\!\!\text{ }$ centered at O. Let p be a point inside the spherical shell at a distance r from the center of the spherical shell.
Draw two planes CD and EF perpendicular to OP and very close to each other. The area in between these two planes will act as a ring of radius EG and width CE.
If $\angle EOB=\theta \text{ and }\angle COE=d\theta $, then the radius of the circle is given by, $EG=OE\sin \theta =R\sin \theta $. The width of the ring is given by, $CE=Rd\theta $.
$\text{Area of Ring}=\text{Circumference}\times \text{Width}$
$\Rightarrow \text{Area of Ring}=2\pi R\sin \theta \times Rd\theta $
$\therefore \text{Area of Ring}=2\pi {{R}^{2}}\sin \theta d\theta $
Mass of the ring can be calculated by multiplying the area of the ring with the surface mass density.
$\text{Mass of the Ring}=2\pi {{R}^{2}}\sin \theta d\theta \times \sigma $
$\therefore \text{Mass of the Ring}=2\pi {{R}^{2}}\sigma \sin \theta d\theta $
Since every point of the ring is at the same distance x from the point P, the small potential $\text{dV at P}$ due to the ring is given by,
$dV=-G\dfrac{\text{Mass of the Ring}}{x}$
$dV=-G\dfrac{2\pi {{R}^{2}}\sigma \sin \theta d\theta }{x}$ … equation (1)
In triangle OEP, $\text{E}{{\text{P}}^{\text{2}}}=\text{O}{{\text{E}}^{\text{2}}}+\text{O}{{\text{P}}^{\text{2}}}-\text{2}\text{.OE}\text{.OP}\text{.cos }\!\!\theta\!\!\text{ }$, which can be written as
${{x}^{2}}={{R}^{2}}+{{r}^{2}}-2Rr\cos \theta $
Differentiating the above equation, we get,
$2x=2Rr\sin \theta d\theta $
$\therefore \sin \theta d\theta =\dfrac{x}{Rr}dx$
Substituting the above relation in equation (1), we get,
$dV=-G\dfrac{2\pi R\sigma }{r}dx$ … equation (2)
To obtain the potential V at P for the whole shell, we will integrate the above expression for dV between the limits $BP=R-r\text{ and }AP=R+r$.
$\therefore V=\int_{R-r}^{R+r}{-G\dfrac{2\pi R\sigma }{r}}dx$
Integrating and applying the limits to the above integral we get,
$V=-G\dfrac{2\pi R\sigma }{r}\left[ 2r \right]=-G\dfrac{4\pi {{R}^{2}}\sigma }{R}$
We know that $4\pi {{R}^{2}}$ is the surface area of the sphere. So, $4\pi {{R}^{2}}\sigma $ is the mass M of the shell.
$\therefore V=-\dfrac{GM}{R}$ … equation (3)
This value is similar to the value of the potential at the surface of the shell. So we can conclude that the potential inside the spherical shell is constant.
The force acting on the point P can be found out by differentiating the potential at P by r.
$F=-\dfrac{dV}{dr}=-\dfrac{d}{dr}\left[ -\dfrac{GM}{R} \right]$
Since the potential is a constant inside the shell, we will get,
$\therefore F=0$
So, the gravitational field inside the spherical shell is zero.
So, the answer to the question is both the options (B) and (C).

Note: The gravitational potential of a spherical shell of mass M and radius R at a distance r along the axis is given by, $V=-\dfrac{GM}{r}$. The gravitational field for the same point is $F=-\dfrac{GM}{{{r}^{2}}}$.
The gravitational potential of a spherical shell of mass M and radius R on the surface of the shell is given by, $V=-\dfrac{GM}{R}$. The gravitational field for the same point is $F=-\dfrac{GM}{{{R}^{2}}}$.