Question

In $\vartriangle ABC,m\angle B = {90^ \circ },AB = 4$ and $BC = 3$, then the radius of the circle touching all three vertices of a triangle will be?
A. 2.5
B. 2
C. 3.5
D. 3

Answer 1

Hint: We will first see that ABC will be a right angled triangle. So, we can apply the Pythagorean Theorem here and then by applying the Pythagorean Theorem, we will have our answer.

Complete step-by-step answer:
Let us first know the types of triangle:-
Acute angled triangle: A triangle with all angles less than ${90^ \circ }$.
Obtuse angled triangle: A triangle with one angle greater than ${90^ \circ }$.
Right angled triangle: A triangle with one angle equal to ${90^ \circ }$.
Now, in the question given to us the measure of angle B is ${90^ \circ }$. Hence, $\vartriangle ABC$ is a right angled triangle.
Now, we have heard about the Pythagorean Theorem which says that in a right angled triangle, the square of the hypotenuse is equal to the sum of squares of the two other sides.
This implies that: \[{H^2} = {P^2} + {B^2}\], where H is the length of hypotenuse, P is the length of perpendicular and B is the length of base of the triangle.
Let us draw the triangle for our reference:

               

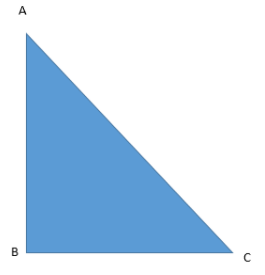
Here, AB = 4 and BC = 3.
Applying Pythagorean on this will give us:-
\[A{C^2} = A{B^2} + B{C^2}\]
\[A{C^2} = {3^2} + {4^2} = 25\]
So, \[AC = 5\].
Now, let us draw circle over it as follows:

               

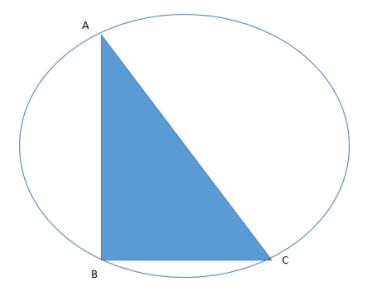
We also know that the angle in a circle is semi-circle. Therefore, the triangle ABC lies in the semi-circle and hence AC is the diameter of the circle.
Therefore the radius of the circle must be half its length.
Hence, $Radius = \dfrac{{AC}}{2} = \dfrac{5}{2} = 2.5$.

So, the correct answer is “Option A”.

Note: The students must note that AC is a diameter of the circle is very clear from the picture but they cannot use it as the argument. They need to give a proper reason as in comparison to vague pictures.
The students must also remember that they can use the Pythagorean Theorem only on right angled triangles. If given any other kind of triangle, you may draw an altitude to use the Pythagorean Theorem.