Question

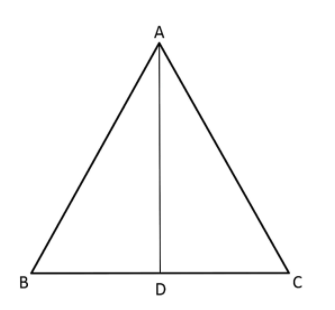
In triangle $\vartriangle $ ABC, AD is perpendicular to BC and \[A{D^2} = {\text{ }}BD \times DC\]. Prove that angle \[\angle BAC{\text{ }} = {\text{ }}90^\circ \].

Answer 1

Hint: Apply Pythagoras theorem in right angled $\vartriangle ADC \& \vartriangle ABD$ and make equations of relation between different sides of the triangle in such a way that we can apply converse of Pythagoras theorem to prove \[\angle BAC{\text{ }} = {\text{ }}90^\circ \]

Complete step by step solution:
In right angle triangle $\vartriangle ABD$, $AD$ is perpendicular to $BC$, $AD \bot BC$
$\angle ABD = \angle ADC = 90^\circ $
Required to prove: \[\angle BAC{\text{ }} = {\text{ }}90^\circ \]
To prove, we will have to apply Pythagoras theorem in right angled triangle $\vartriangle ADC\& \vartriangle ABD$
Pythagoras' Theorem states that, for any right-angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the two shorter sides.
By applying Pythagoras theorem in right angled $\vartriangle $ADB,
${\text{Hypotenuse}}^2 = {\text{Perpendicular}}^2 + {\text{Base}}^2$
 $ \Rightarrow A{B^2} = A{D^2} + B{D^2}$
$ \Rightarrow A{D^2} = A{B^2} - B{D^2}$…………………. (1)
By applying Pythagoras theorem in right angled $\vartriangle $ADC,
\[\;A{C^2} = A{D^2} + C{D^2}\]
\[\; \Rightarrow A{D^2} = A{C^2} - C{D^2}\]………………… (2)
Adding equation (1) & (2),
\[\; \Rightarrow A{C^2} - C{D^2} + A{B^2} - B{D^2} = 2A{D^2}\]$ \Rightarrow B{D^2} + C{D^2} + 2\left( {BD \times DC} \right)$
Simplifying the above equation,
$ \Rightarrow B{D^2} + C{D^2} + 2\left( {BD \times DC} \right) = A{B^2} + A{C^2}$
Arrange \[BC{\text{ }}\& {\text{ }}DC\] terms in the same side
\[ \Rightarrow {\left( {BD + DC} \right)^2} = A{B^2} + A{C^2}\]
By applying \[\left[ {{\text{ }}BD{\text{ }} + {\text{ }}DC{\text{ }}={\text{ }}BC} \right]\]formula,
$\Rightarrow {BC^2} = A{B^2} + A{C^2}$\[\left[ {\because {\text{ }}BD{\text{ }} + {\text{ }}DC{\text{ }} = {\text{ }}BC} \right]\]
By the converse of Pythagoras theorem,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
[As longest side of triangle ABC is $BC$ & other two sides are $AB$ and $AC$]

\[\therefore \angle BAC{\text{ }} = {\text{ }}90^\circ \]. Hence proved.

Note:
First of all, make a relatable diagram and then equations relating different sides of the triangle. We need to have concepts of converse of Pythagoras theorem to prove that \[\angle BAC{\text{ }} = {\text{ }}90^\circ \]