Question

In triangle PQR, right angled at Q, \[PR + QR = 25\] cm and \[PQ = 5\] cm. Find all the sides of the triangle.

Answer 1

Hint:
Here, we need to find the sides of the triangle. One side of the triangle is already given. Using the given information, Pythagoras’s theorem, and algebraic identities, we will find the other two sides of the right angled triangle PQR.

Formula Used:
The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\text{Hypotenus}}{{\text{e}}^2} = {\text{Perpendicula}}{{\text{r}}^2} + {\text{Bas}}{{\text{e}}^2}\].

Complete step by step solution:
First, let us draw the given right angled triangle PQR.

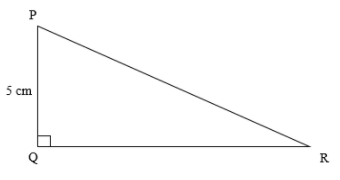
It is given that the sum of the sides PR and QR is 25 cm, that is \[PR + QR = 25\] cm.
Rewriting the equation, we get
\[ \Rightarrow PR = 25 - QR\]
Now, we will use the Pythagoras’s theorem in the right angled triangle PQR.
The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\text{Hypotenus}}{{\text{e}}^2} = {\text{Perpendicula}}{{\text{r}}^2} + {\text{Bas}}{{\text{e}}^2}\].
From the figure, we can observe that PQ is the perpendicular of the right angled triangle, QR is the base of the right angled triangle, and PR is the hypotenuse of the right angled triangle.
Therefore, using the Pythagoras’s theorem in right angled triangle PQR, we get
\[ \Rightarrow P{R^2} = P{Q^2} + Q{R^2}\]
Substituting \[PQ = 5\] cm and \[PR = 25 - QR\] in the equation, we get
\[ \Rightarrow {\left( {25 - QR} \right)^2} = {5^2} + Q{R^2}\]
Using the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], we can simplify the equation as
\[ \Rightarrow {\left( {25} \right)^2} + Q{R^2} - 2\left( {25} \right)\left( {QR} \right) = {5^2} + Q{R^2}\]
Applying the exponents on the bases, we get
\[ \Rightarrow 625 + Q{R^2} - 2\left( {25} \right)\left( {QR} \right) = 25 + Q{R^2}\]
Multiplying the terms in the expression, we get
\[ \Rightarrow 625 + Q{R^2} - 50QR = 25 + Q{R^2}\]
Subtracting \[Q{R^2}\] from both sides of the equation, we get
$ \Rightarrow 625 + Q{R^2} - 50QR - Q{R^2} = 25 + Q{R^2} - Q{R^2} \\
   \Rightarrow 625 - 50QR = 25 \\ $
Subtracting 25 from both sides of the equation, we get
$ \Rightarrow 625 - 50QR - 25 = 25 - 25 \\
   \Rightarrow 600 - 50QR = 0 \\ $
Rewriting the expression, we get
\[ \Rightarrow 50QR = 600\]
Dividing both sides of the equation by 50, we get
$ \Rightarrow \dfrac{{50QR}}{{50}} = \dfrac{{600}}{{50}} \\
  \therefore QR = 12 \\ $
Thus, we get the length of base QR is 12 cm.
Now, substituting \[QR = 12\] cm in the equation \[PR = 25 - QR\], we get
\[ \Rightarrow PR = 25 - 12\]
Subtracting the terms, we get
\[\therefore PR = 13\]
Thus, we get the length of hypotenuse PR as 13 cm.

Therefore, the sides of the triangle are of lengths 5 cm, 12 cm, and 13 cm.

Note:
We used the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\] in the solution. The square of the difference of two numbers \[a\] and \[b\] is given by the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\].
We obtained the sides of the triangle as 5 cm, 12 cm, and 13 cm. The numbers 5, 12, 13 are called Pythagorean triples because they satisfy the Pythagoras’s theorem.
We can also solve the problem by rewriting the sum of PR and QR as \[QR = 25 - PR\], and then substituting \[QR = 25 - PR\] in the equation \[P{R^2} = P{Q^2} + Q{R^2}\].