Question

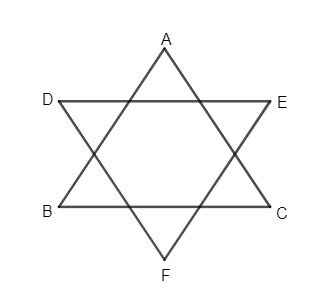
In the given figure, what is the value of $\angle A+\angle B+\angle C+\angle D+\angle E+\angle F$ ?

(a) $360{}^\circ $
(b) $270{}^\circ $
(c) $540{}^\circ $
(d) $180{}^\circ $

Answer 1

Hint: Use the fundamental property of a triangle that the sum of all the interior angles of a triangle is $180{}^\circ $. See the triangles ABC and DEF individually to calculate the given expression in the problem.

Complete Step-by-Step solution:
As we know that we do not have any angles of A, B, C, or D, E, F or any other in the problem. So, we need to use some property to get the value of $\angle A+\angle B+\angle C+\angle D+\angle E+\angle F$.
Now, we can observe that ABC and DEF both are triangles if we see them individually or by separating them. So, we get diagram as

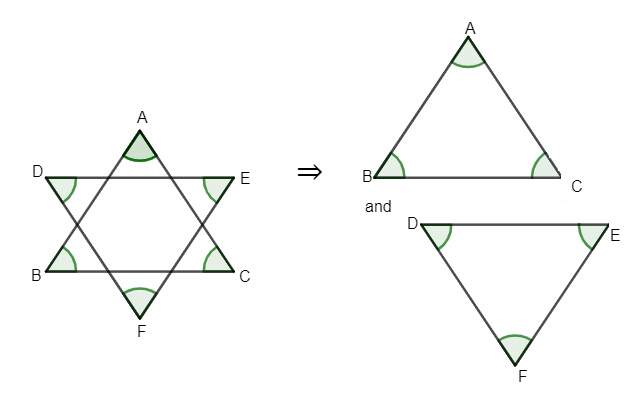
Now, we can notice that angles A, B, C belong to triangle ABC only and angles D, E, F belong to triangle DEF. So, we need to use the fundamental property of a triangle which is given as
“ Sum of all interior angles of a triangle is $180{}^\circ $. “
So, the sum of angles of $\Delta ABC$ is $180{}^\circ $ and the sum of angles of $\Delta DEF$ is $180{}^\circ $ as well.
So, we can represent the sum of angles of both the triangles in mathematical equations. So, we get
$\angle A+\angle B+\angle C=180{}^\circ $ ……………………………..(i)
$\angle D+\angle E+\angle F=180{}^\circ $ ………………………………..(ii)
Now, add the equations (i) and (ii) to get the sum of angles required in the problem.
So, after adding equation (i) and (ii), we get
$\angle A+\angle B+\angle C+\angle D+\angle E+\angle F=180{}^\circ +180{}^\circ $
$\angle A+\angle B+\angle C+\angle D+\angle E+\angle F=360{}^\circ $
Hence, the sum of all these angles given in the problem is $360{}^\circ $. So, option (A) is the correct answer.

Note: Don’t go for calculating the exact values of $\angle A,\angle B,\angle C,\angle D,\angle E$ or $\angle F$. As it is not possible to calculate any of them as we do not know any of the angles given in the expression of the problem. So, using the fundamental property of triangles is the key point of the question.
One may go wrong and get confused with the sum of angles of a triangle and may put the sum as $90{}^\circ $ or $360{}^\circ $ or any other value. So be careful and remember that sum of all angles of a triangle is $180{}^\circ $ and remember the below identity to calculate sum of angles of any polygon :-
$=\left( n-2 \right)\times 180$
Where n = Number of sides/vertices of the polygon.