Question

In the given figure two poles of height a meters and b meters are p meters apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by $\dfrac{{{\text{ab}}}}{{{\text{a + b}}}}$meters.

Answer 1

Hint – To prove the height, we observe the figure and using the properties of triangles we compare them and establish a relationship between the distance between the poles and the height. We then simplify the relation to prove the height.

Complete step-by-step answer:

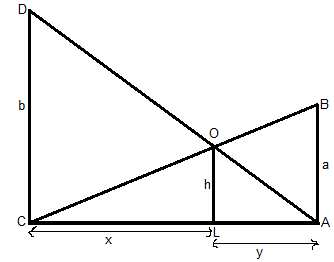
Let AB and CD be two poles of heights a meters and b meters respectively such that the poles are p meters apart i.e. AC = p meters. Let us suppose the lines AD and BC meet at O such that OL = h meters.
Let CL = x and LA = y, then x + y = p.
In ∆ABC and ∆LOC, we have
∠CAB = ∠CLO -- (equal to 90°)
∠C = ∠C -- (common angle for both triangles)
We know, the AA Similarity Postulate says that two triangles are similar if two angles in a triangle are congruent to two angles in another.
∴∆CAB ~ ∆CLO -- (By AA criterion of similarity)
$
   \Rightarrow \dfrac{{{\text{CA}}}}{{{\text{CL}}}} = \dfrac{{{\text{AB}}}}{{{\text{LO}}}} \\
   \Rightarrow \dfrac{{\text{p}}}{{\text{x}}} = \dfrac{{\text{a}}}{{\text{h}}} \\
   \Rightarrow {\text{x = }}\dfrac{{{\text{ph}}}}{{\text{a}}}{\text{ - - - - (1)}} \\
$

Now in ∆ALO and ∆ACD, we have
∠ALO = ∠ACD -- (both are equal to 90° from the figure)
∠A = ∠A -- (common angle)
∴∆ALO ~ ∆ACD -- (By AA criterion of similarity)
⟹$
   \Rightarrow \dfrac{{{\text{AL}}}}{{{\text{AC}}}} = \dfrac{{{\text{OL}}}}{{{\text{DC}}}} \\
   \Rightarrow \dfrac{{\text{y}}}{{\text{p}}} = \dfrac{{\text{h}}}{{\text{b}}} \\
   \Rightarrow {\text{y = }}\dfrac{{{\text{ph}}}}{{\text{b}}}{\text{ - - - - (2)}} \\
$

Now from (1) and (2) we have
x + y = $\dfrac{{{\text{ph}}}}{{\text{a}}} + \dfrac{{{\text{ph}}}}{{\text{b}}}$
We know x + y = p, hence the equation becomes
$
   \Rightarrow {\text{p = ph}}\left( {\dfrac{1}{{\text{a}}} + \dfrac{1}{{\text{b}}}} \right) \\
   \Rightarrow 1 = {\text{ h}}\left( {\dfrac{{{\text{a + b}}}}{{{\text{ab}}}}} \right) \\
   \Rightarrow {\text{h = }}\dfrac{{{\text{ab}}}}{{{\text{a + b}}}}{\text{meters}} \\
$
Hence, the height of the intersection of the lines joining the top of each pole to the foot of the opposite pole is $\dfrac{{{\text{ab}}}}{{{\text{a + b}}}}$meters.
Hence Proved.

Note – In order to solve this type of problems the key is to construct a figure with given data and we assume a height h and point L in the figure for our convenience. A good knowledge in triangles and their properties is appreciated. The angles ∠BAC and ∠ACD are 90° because poles are generally placed vertical to the ground, also height refers to the perpendicular distance from a point.Students should remember theorems and postulates for solving these type of problems.