Question

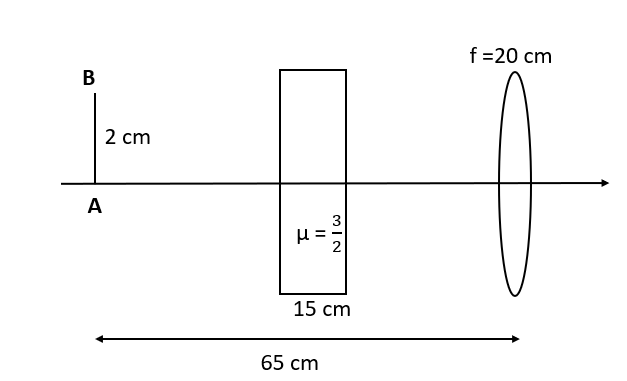
In the given figure, the image of object AB observed by observer is:

Answer 1

Hint: The image distance can be measured with the information of object length and focal length with the aid of the lens formula. In optics, the connection between the image distance (i), the object distance (u), and the focal length (f) are provided by the formula identified as the Lens formula. The lens formula is suitable for convex and concave lenses. These lenses have almost negligible thickness.

Complete step-by-step solution:
Given: A plate of thickness $t = 15 cm$ is inserted in between the lens.
Refractive index of plate is $\mu = \dfrac{3}{2}$
Object’s distance, $u = 65 cm$
Focal length, $f = 20 cm$
There is shift in the object distance due to insertion of plate.
Shift, $s = t \left(1 - \dfrac{1}{\mu} \right)$
After putting the value of thickness and refractive index. We get,
$s = 15 \left(1 - \dfrac{2}{3} \right) = 5 cm$
We need to subtract shift distance from object’s distance.
Then, object distance will be $65 – 5 = 60 cm$
Apply Len’s formula,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Put $f = 20 cm; u =- 60 cm $
$\dfrac{1}{20} = \dfrac{1}{v} - \dfrac{1}{-60}$
$\dfrac{1}{20} - \dfrac{1}{60} = \dfrac{1}{v}$
$ \dfrac{1}{v} = \dfrac{3-1}{60}$
We get, $v = 30 cm$.
Hence, the image of object AB observed by the observer is $30 cm$.

Note: The lens formula applies to all sites with suitable sign conventions. This lens formula applies to both the convex and concave lens. If the equation explains a negative image length, then the image is a practical image on the corresponding side of the lens while the object. If this equation gives a negative focal length, then the lens is a divergent lens rather than the convergent lens. This equation is utilized to obtain image distance for both real or virtual images.