Question

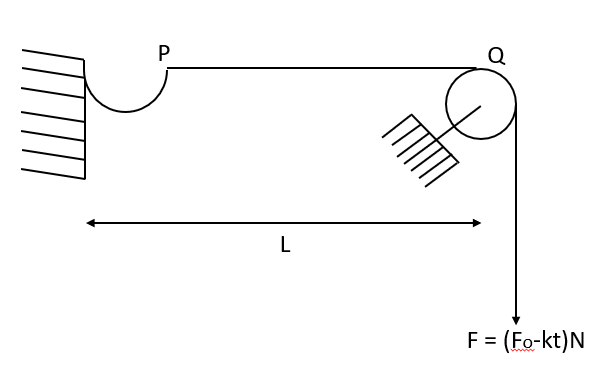
In the given figure a string of linear mass density m and length L is stretched by a force \[F=(Fo-kt)N\] where $Fo$ & k are constant and t is time t = 0, a pulse is generated at the end P of the string. As the pulse reaches the point Q, the force vanishes. The value of K in the above equation is

Answer 1

Hint: Firstly, we will find the value of the time for the pulse to reach the end Q of the string by putting F=0 in the given expression for the force \[F={{F}_{0}}-kt\].Then, using the formula for the velocity of wave in a stretched string, that is \[V=\sqrt{\dfrac{T}{m}}~\]. We can find the expression for the velocity of the pulse. Finally, substituting $v=\dfrac{dx}{dt}$and integrating the resulting expression, we will get the required value of the constant k.

Formula Used: \[V=\sqrt{\dfrac{T}{m}}~\]
Where T is Tension, V is Velocity and m is linear mass density of the string.

Complete step-by-step solution:
Tension in the string is, \[T={{F}_{0}}-kt\]
et the velocity of pulse in the string is 'V' and the time take by the pulse to travel distance from P to Q is \[{{t}_{0}}\].​ Then at time \[{{t}_{0}}\]​,
 $0={{F}_{0}}$
\[0={{F}_{0}}-k{{t}_{0}}\]
Hence,\[{{t}_{0}}=\dfrac{{{F}_{0}}}{K}\]
Now, \[V=\sqrt{\dfrac{T}{m}}~\]
Therefore,\[~\dfrac{dx}{dt}=\sqrt{\dfrac{{{F}_{0}}kt}{m}}\]
\[\int _{0}^{L}dx=\dfrac{1}{\sqrt{m}}\int _{0}^{{{t}_{0}}}{{({{F}_{0}}-kt)}^{1/2}}dt\]
\[L=\dfrac{1}{\sqrt{m}}\times \dfrac{-2}{3k}[{{({{F}_{0}}-kt)}^{3/2}}]_{0}^{{{t}_{0}}}\]
\[L=\dfrac{-2}{3k\sqrt{m}}[0-F_{0}^{3/2}]\]
\[K=\dfrac{2F_{0}^{3/2}}{3L\sqrt{m}}\]
After solving. We get value of\[K=\dfrac{2}{3L}\sqrt{\dfrac{F_{0}^{3}}{m}}\]
Hence, the value of K in the equation \[F=(Fo-kt)N\] is \[K=\dfrac{2}{3L}\sqrt{\dfrac{F_{0}^{3}}{m}}\]

Note: Since, velocity 'V' is not constant with time as it is Varying with time. Also, time is not being calculated along with the pulse by \[\dfrac{dis\tan ce}{speed}\] formula because velocity ‘V’ is not constant. That’s why we are using \[V=\sqrt{\dfrac{T}{m}}~\].After Integration, we will get the value of k.