Question

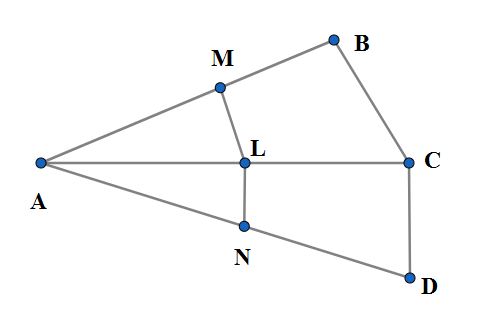
In the following figure $LM||CB$and $LN||CD$, prove that $\dfrac{AM}{AB}=\dfrac{AN}{AD}$. \[\]

Answer 1

Hint: We recall the proportionality theorem in triangles which states that when a line is drawn parallel to any one side of a triangle in such a way that it intersects the other two sides in two distinct points then the other two sides of the triangle are divided in the same ratio. We use the proportionality theorem in triangle ABC and ACD to get $\dfrac{MB}{AM}=\dfrac{ND}{AN}$. We add 1 both sides and simplify to prove the given statement.

Complete step-by-step answer:
We know from proportionality theorem of triangles that when a line is drawn parallel to any one side of a triangle in such a way that it intersects the other two sides in two distinct points then the other two sides of the triangle are divided in the same ratio at the two distinct points, for example in triangle PQR below line parallel to QR cuts the side PQ at the point X and cut the side QR at the point Y. \[\]
 

We use proportionality theorem and conclude that PQ is divided at X at the same ratio as PR is divided at Y which means
\[\dfrac{PX}{QX}=\dfrac{PY}{RY}\]
Let us observe the triangle ABC in the given figure. W are given in the question $LM||CB$. So we use proportionality theorem and conclude that LM divides the sides AB and AC in the same ratio at the points M and L respectively which means;
\[\dfrac{AM}{MB}=\dfrac{AL}{LC}.....\left( 1 \right)\]
Let us observe the triangle ACD in the given figure. W are given in the question $LN||CD$. So we use proportionality theorem and conclude that LN divides the sides AC and AD in the same ratio at the points L and N respectively which means;
 \[\dfrac{AL}{LC}=\dfrac{AN}{ND}.....\left( 2 \right)\]
We have from (1) and (2)
\[\dfrac{AM}{MB}=\dfrac{AN}{ND}\]
We use invertendo property of ratio to have;
\[\dfrac{MB}{AM}=\dfrac{ND}{AN}\]
We add 1 both side to have;
\[\begin{align}
  & \Rightarrow \dfrac{MB}{AM}+1=\dfrac{ND}{AN}+1 \\
 & \Rightarrow \dfrac{MB+AM}{AM}=\dfrac{ND+AN}{AN} \\
 & \Rightarrow \dfrac{AB}{AM}=\dfrac{AD}{AN} \\
\end{align}\]
We use invertendo property of ratio again to have;
\[\Rightarrow \dfrac{AM}{AB}=\dfrac{AN}{ND}\]
Hence the given statement is proved.

Note: We can alternatively solve using the similarity of triangles. We prove the similarity of triangles ALM and ABC $\dfrac{AM}{MB}=\dfrac{AL}{LC}$, then we prove the similarity of triangles ALN and ACD to get $\dfrac{AL}{LC}=\dfrac{AN}{ND}$ and then proceed like we have in the solution. The invertendo property of ratio is $\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow \dfrac{b}{a}=\dfrac{c}{d}$ where $a,b,c,d$ cannot be zero.