Question

In the figure shown, what is the value of $v + x + y + z + w$?

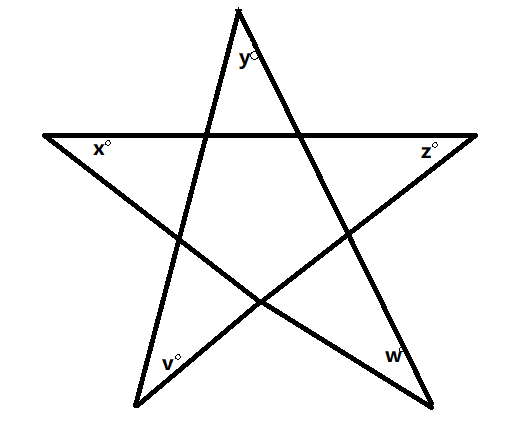
A. 45
B. 90
C. 180
D. 270
E. 360

Answer 1

Hint: The figure consists the shape of a pentagon. The sum of the interior angles of a pentagon is equal to ${540^ \circ }$. Use the angle sum property of a triangle including the one angle of the pentagon to formulate relations. Solve the relations to find the required value.

Complete step by step Answer:

Let the given figure be labeled as follows.

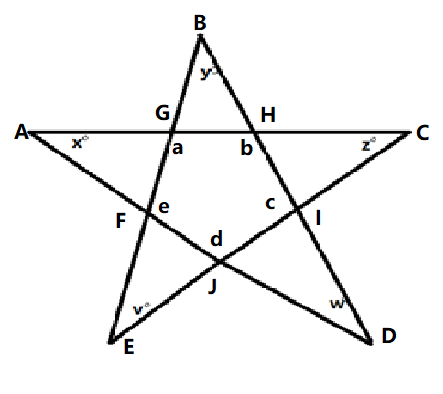
The polygon formed by the $FGHIJ$ is a pentagon and has 5 sides.
The sum of the interior angles of a polygon with $n$ sides is given by $\left( {n - 2} \right){180^ \circ }$.
Thus the sum of the interior angles of the polygon $FGHIJ$ is given by substituting the value 5 for $n$ in the relation $\left( {n - 2} \right){180^ \circ }$.
$
  \left( {5 - 2} \right){180^ \circ } \\
   \Rightarrow {540^ \circ } \\
 $
For the given figure the sum of the interior angles of the polygon $FGHIJ$ is given by $a + b + c + d + e$
Thus, we can say that $a + b + c + d + e = {540^ \circ }$ .
Consider the triangle $\vartriangle ACJ$, by using the angle sum property of a triangle, we have all the angles of any triangle is equal to ${180^ \circ }$
That is, $x + z + d = {180^ \circ }$
Similarly, relations can be formed for the other angles of the pentagon.
$c + y + v = {180^ \circ }$
$x + w + b = {180^ \circ }$
$a + v + z = {180^ \circ }$
$e + y + w = {180^ \circ }$
Adding the above five equations ,we get
$a + b + c + d + e + 2\left( {x + y + z + w + v} \right) = {900^ \circ }$
Substituting the value ${540^ \circ }$ for $a + b + c + d + e$ in the above equation
$
  2\left( {x + y + z + w + v} \right) = {360^ \circ } \\
   \Rightarrow x + y + z + w + v = {180^ \circ } \\
$
Thus, option C is the correct answer.

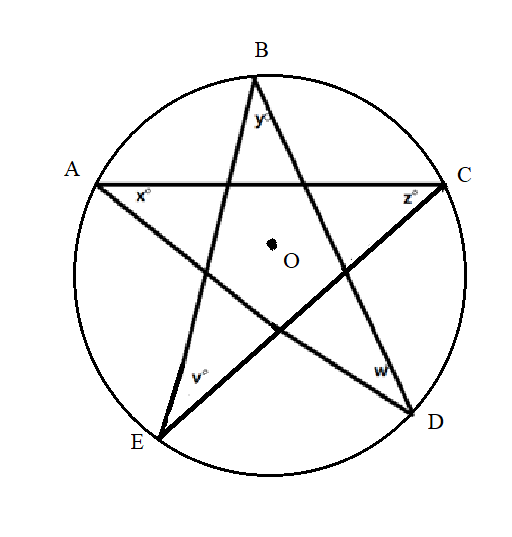
Note: Also, if the angles given in the figure are equal, then each angle is equals to $\dfrac{{180}}{5} = {36^ \circ }$. Alternatively, we can also find the value of the required angles by assuming a circle around the given figure, then there are five equal arcs subtending an angle of $\dfrac{{360}}{5} = {72^ \circ }$ at the center. And we can see that at the vertex A the angle is subtended by the arc CD which is $\dfrac{{72}}{2} = {36^ \circ }$. There are five such angles in the figure, hence the sum is $5 \times 36 = {180^ \circ }$