Question

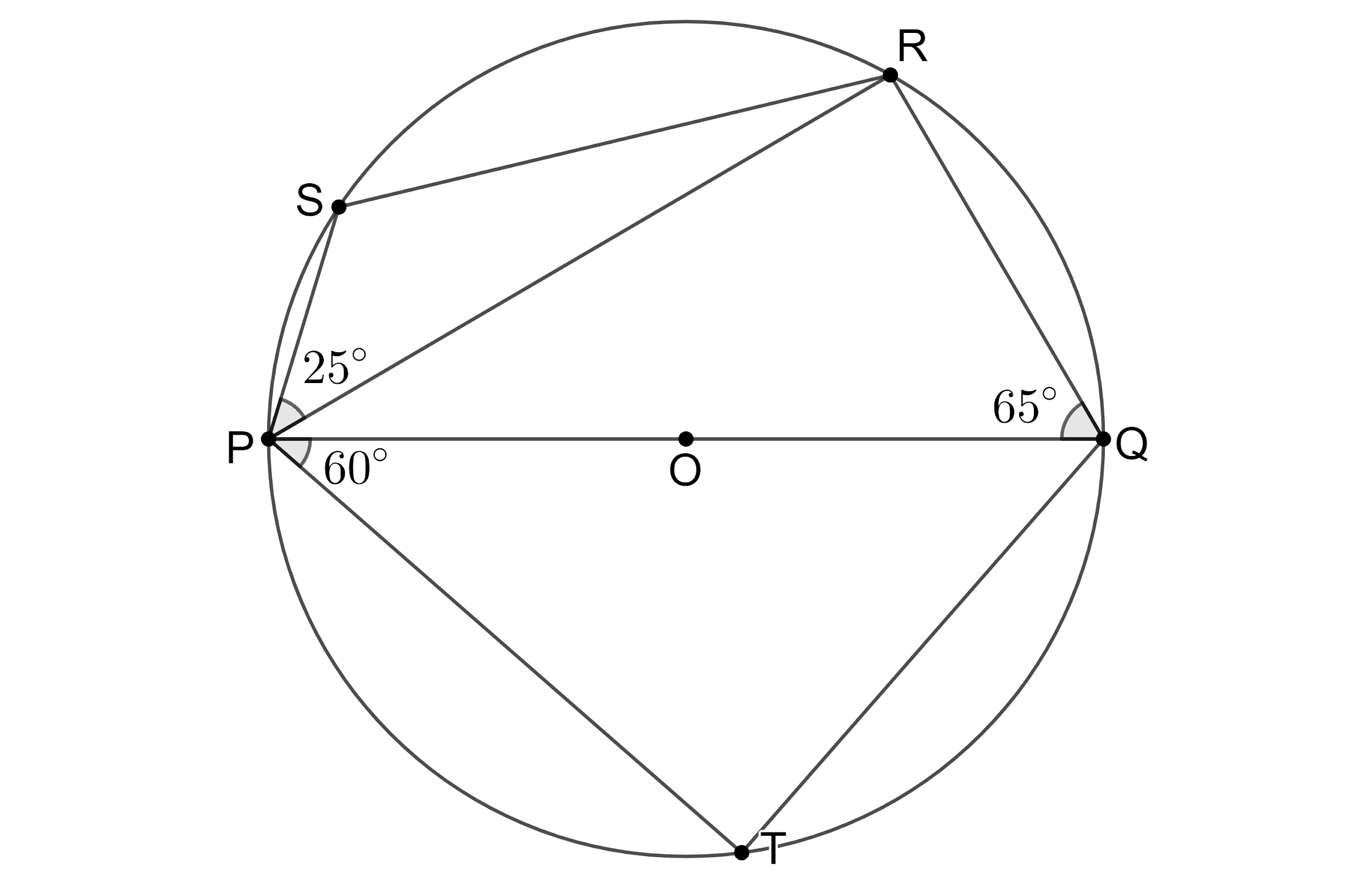
In the figure, PQ is the diameter of the circle. If $ \angle PQR={{65}^{\circ }} $ , $ \angle RPS={{25}^{\circ }} $ and $ \angle QPT={{60}^{\circ }} $ , then find the measure of (i) $ \angle QPR $ , (ii) $ \angle PRS $ , (iii) $ \angle PSR $ and (iv) $ \angle PQT $ ?

Answer 1

Hint: We start solving the problem by making use of the fact that angle in a semicircle is $ {{90}^{\circ }} $ to find the value of angle $ \angle QTP $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PQT to find the angle $ \angle PQT $ . We then make use of the fact that angle in a semicircle is $ {{90}^{\circ }} $ to find the value of angle $ \angle QRP $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PQR to find the angle $ \angle QPR $ . We then make use of the fact that the sum of opposite angles in a concyclic polynomial is $ {{180}^{\circ }} $ to find the angle $ \angle PSR $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PRS to find the angle \[\angle PRS\].

Complete step by step answer:
According to the problem, we are given that PQ is the diameter of the circle. If $ \angle PQR={{65}^{\circ }} $ , $ \angle RPS={{25}^{\circ }} $ and $ \angle QPT={{60}^{\circ }} $ . We need to find the values of the angles (i) $ \angle QPR $ , (ii) $ \angle PRS $ , (iii) $ \angle PSR $ and (iv) $ \angle PQT $ .
Let us redraw the given figure,

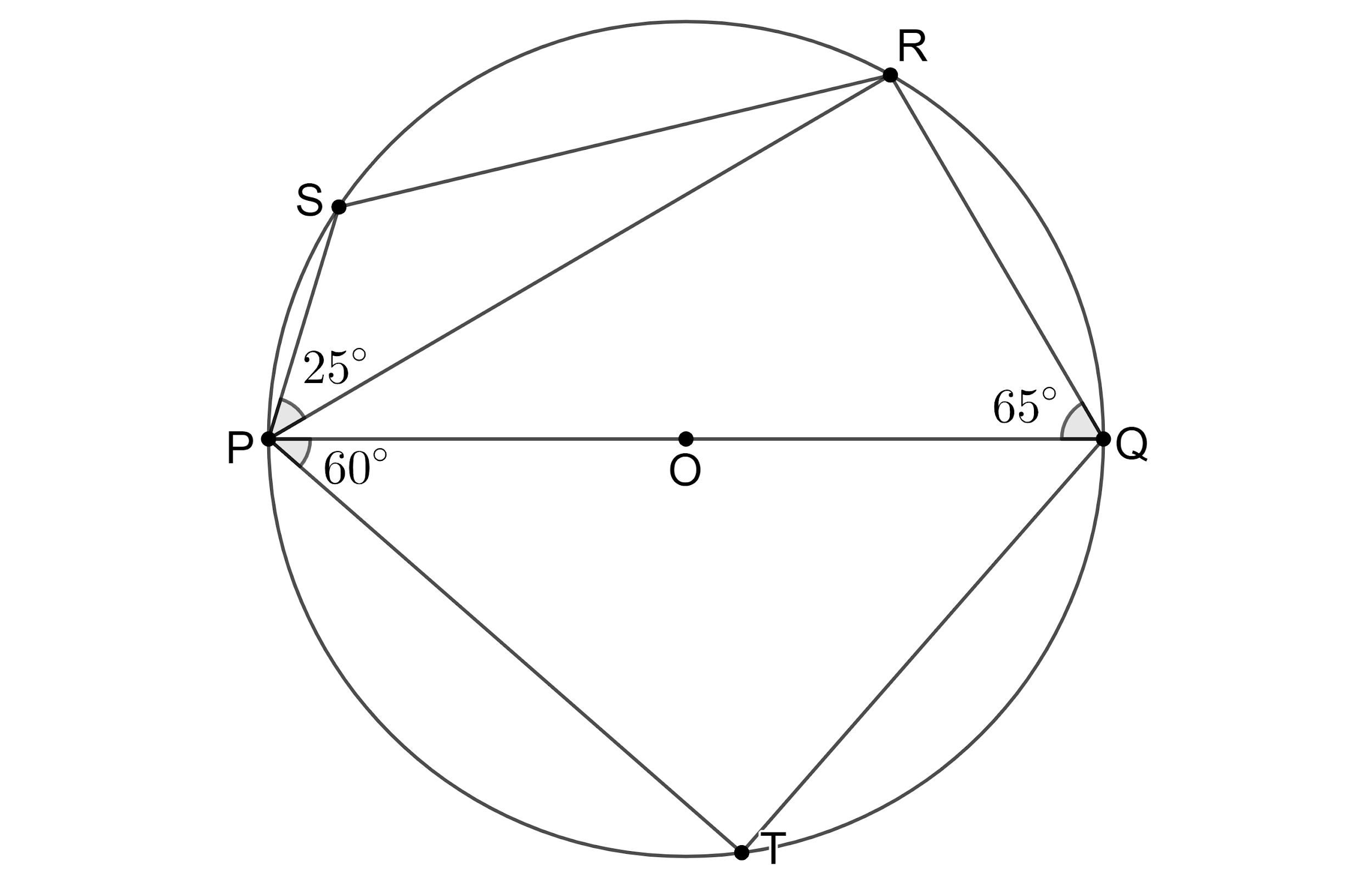
From the figure, we can see that $ \angle QTP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QTP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ so, we get $ \angle QTP={{90}^{\circ }} $ ---(1).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQT $ , we have $ \angle QTP+\angle TPQ+\angle PQT={{180}^{\circ }} $ .
From equation (1), we get
 $ \Rightarrow {{60}^{\circ }}+{{90}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
 $ \Rightarrow {{150}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
 $ \Rightarrow \angle PQT={{30}^{\circ }} $ .
From the figure, we can see that $ \angle QRP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QRP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ , so we get $ \angle QRP={{90}^{\circ }} $ ---(2).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQR $ , we have $ \angle PQR+\angle QRP+\angle QPR={{180}^{\circ }} $ .
From equation (2), we get
 $ \Rightarrow {{65}^{\circ }}+{{90}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
 $ \Rightarrow {{155}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
 $ \Rightarrow \angle QPR={{25}^{\circ }} $ .
We can see that the points P, Q, R, S form a concyclic quadrilateral. We know that the sum of opposite angles in a concyclic polynomial is $ {{180}^{\circ }} $.
So, we have $ \angle PQR+\angle PSR={{180}^{\circ }} $ .
 $ \Rightarrow {{65}^{\circ }}+\angle PSR={{180}^{\circ }} $ .
 $ \Rightarrow \angle PSR={{115}^{\circ }} $ ---(3).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From triangle $ PSR $ , we have $ \angle PSR+\angle PRS+\angle RPS={{180}^{\circ }} $ .
From equation (3), we get
 $ \Rightarrow {{25}^{\circ }}+{{115}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
 $ \Rightarrow {{140}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
 $ \Rightarrow \angle PRS={{40}^{\circ }} $ .
 $ \therefore $ We have found the values of angles $ \angle QPR $ , $ \angle PRS $ , $ \angle PSR $ and $ \angle PQT $ as $ {{25}^{\circ }} $ , $ {{40}^{\circ }} $ , $ {{115}^{\circ }} $ and $ {{30}^{\circ }} $ .

Note:
We can see that the given problem contains a huge amount of calculations, so we need to perform each step carefully to avoid confusion. We should not confuse angles while using the property of angle in a semi-circle. We should not make calculation mistakes while solving this problem. Whenever we get this type of problem, we should make use of properties of concyclic polygons and angle in a semi-circle to get the required answer.