Question

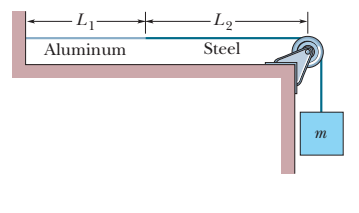
In the Figure, an aluminum wire, of length \[{L_1} = 60.0cm\] cross-sectional area\[1.00 \times {10^{ - 2}}c{m^2}\], and density\[2.60g/c{m^3}\], is joined to a steel wire, of density \[7.80g/c{m^3}\] and the same cross-sectional area. The compound wire, loaded with a block of mass\[m = 10.0kg\], is arranged so that the distance \[{L_2}\]​from the joint to the supporting pulley is\[86.6cm\]. Transverse waves are set up on the wire by an external source of variable frequency; a node is located at the pulley. Find the lowest frequency that generates a standing wave having the joint as one of the nodes.

Answer 1

Hint: From the question, we absorbed that the length, cross-sectional area, and density are given for two sections. And also the mass of the loaded block is given. By using these data, first, we have to calculate the ratio of integers. After that, we will find the lowest frequency that generates a standing wave having the joint as one of the nodes.

Complete step by step answer:
The frequencies of the wave for both sections of the wire are the same. The wave speed and wavelength are different in different sections.
Suppose there are \[{n_1}\] loops in the aluminum section of the wire, then
\[{L_1} = \dfrac{{{n_1}{\lambda _1}}}{2} = \dfrac{{{n_1}{v_1}}}{{2f}}\] \[\left( {\therefore {\lambda _1} = \dfrac{{{v_1}}}{f}} \right)\]
Where \[{\lambda _1}\]is the wavelength and \[{v_1}\]is the wave speed in that section.
Thus \[f = \dfrac{{{n_1}{v_1}}}{{2{L_1}}}\]
Similarly, for the steel section \[f = \dfrac{{{n_2}{v_2}}}{{2{L_2}}}\]
We know that the frequency is the same for the two sections \[\dfrac{{{n_1}{v_1}}}{{2{L_1}}} = \dfrac{{{n_2}{v_2}}}{{2{L_2}}}\]
Now, the wave within the aluminum section is given by\[{v_1} = \sqrt {\dfrac{\tau }{{{\mu _1}}}} \], where \[{\mu _1}\]is the linear mass density of the aluminum wire.
The mass of aluminum in the wire is given by \[{m_1} = {\rho _1}A{L_1}\]where \[{\rho _1}\]is the mass density for aluminum and \[A\]is the cross-sectional area of the wire.
\[{\mu _1} = \dfrac{{{\rho _1}A{L_1}}}{{{L_1}}} = {\rho _1}A\] and \[{v_1} = \sqrt {\dfrac{\tau }{{{\rho _1}A}}} \]
Similarly, the wave speed in the steel section \[{v_2} = \sqrt {\dfrac{\tau }{{{\rho _2}A}}} \]
We realized that the cross-sectional area and the tension are the same for the two sections. The equality of the frequency for two sections now leads to\[\dfrac{{{n_1}}}{{{L_1}\sqrt {{\rho _1}} }} = \dfrac{{{n_2}}}{{{L_1}\sqrt {{\rho _2}} }}\]. Where A has been canceled on both sides.
The ratio of the integers \[\dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{{L_2}\sqrt {{\rho _2}} }}{{{L_1}\sqrt {{\rho _1}} }} = \dfrac{{\left( {0.866m} \right)\sqrt {7.80 \times {{10}^3}kg/{m^3}} }}{{\left( {0.600m} \right)\sqrt {2.60 \times {{10}^3}kg/{m^3}} }} = 2.50\]
The smallest integer that has this ratio is \[{n_1} = 2\]and \[{n_2} = 5\]
The frequency is \[f = \dfrac{{{n_1}{v_1}}}{{2{L_1}}} = \left( {\dfrac{{{n_1}}}{{2{L_1}}}} \right)\sqrt {\dfrac{\tau }{{{\rho _1}A}}} \]
The tension provided by the hanging block is\[\tau = mg\]. Where \[m\] is the mass of the block.
Thus, \[f = \dfrac{{{n_1}}}{{{2L_1}}}\sqrt {\dfrac{{mg}}{{{\rho _1}A}}} = \dfrac{2}{{2\left( {0.600m} \right)}}\sqrt {\dfrac{{\left( {10kg} \right)\left( {9.80m/{s^2}} \right)}}{{\left( {2.60 \times {{10}^3}kg/{m^3}} \right)\left( {1.00 \times {{10}^{ - 6}}{m^2}} \right)}}} = 324Hz\]

Note: Steel is harder than aluminum, while rust could be a threat. Steel should be a solid material that’s less likely to warp, deform, or bend when subjected to weight, force, or heat. Nonetheless, steel's resilience comes at the price of being much stronger and denser than aluminum. Steel contains a density of \[2.5\] times that of aluminum.