Question

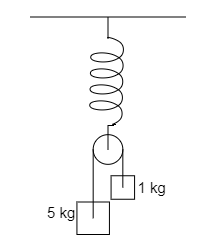
In the figure a smooth pulley of negligible weight is suspended by spring balance $1\,kg$ and $5\,kg$ are attached to the opposite ends of spring passing over pulley and move with acceleration because of gravity. During the motion, spring balance reads weight of?

Answer 1

Hint: The weight act on the spring is determined by solving the two force equation, the two force equation can be written for the two mass $1\,kg$ and $5\,kg$, and by adding this two force equation, the acceleration of the object is determined, then the tension is equal to the sum of the acceleration of the mass and the acceleration due to gravity, then the spring balance reads weight can be determined.

Complete step by step answer:
The two masses which hang on the smooth pulley and the smooth pulley is suspended on the spring, the two masses are $1\,kg$ and $5\,kg$.
The force equation of the $5\,kg$ mass, is written as,
$5a = 5g - T\,.................\left( 1 \right)$
The mass of the object comes down, so the force due to gravity is subtracted by the tension.
The force equation of the $1\,kg$ mass, is written as,
$1a = T - 1g\,.................\left( 2 \right)$
The mass of the object moves upwards, so the tension is subtracted by the force due to gravity.
By adding the equation (1) and the equation (2), then
$5a + 1a = 5g - T + T - 1g$
By adding the terms in the above equation, then the above equation is written as,
$6a = 4g$
By rearranging the terms in the above equation, then the above equation is written as,
$a = \dfrac{{4g}}{6}$
By dividing the terms in the above equation, then the above equation is written as,
$a = \dfrac{{2g}}{3}$
The tension is given by,
$T = a + g$
By substituting the acceleration in the above equation, then
$T = \dfrac{{2g}}{3} + g$
By adding the terms in the above equation, then the above equation is written as,
$T = \dfrac{{5g}}{3}\,N$
The spring will experience the two tension, because the two mass is connected in the spring, then ‘
$ \Rightarrow 2T$
By substituting the tension in the above equation, then
$ \Rightarrow 2 \times \dfrac{{5g}}{3}$
By substituting the acceleration due to gravity in the above equation, then
$ \Rightarrow \dfrac{{2 \times 5 \times 10}}{3}$
By multiplying the terms in the above equation, then the above equation is written as,
$ \Rightarrow \dfrac{{100}}{3}$
By dividing the terms in the above equation, then the above equation is written as,
$ \Rightarrow 33.33\,N$
Thus, during the motion, spring balance reads weight of $33.33\,N$.

Note:The tension of the spring is written as $2T$ because the tension of the spring is due to the two masses. So, the tension of the spring is $2T$. The unit of the tension is equal to the unit of the force, both the tension and the force has the unit newton $N$.