Question

In the dissociation of $PC{l_5}$ as $PC{l_5}(g) \rightleftarrows PC{l_3}(g) + C{l_2}(g)$
If the degree of dissociation is $\alpha $ at equilibrium pressure P, then what is the equilibrium constant for this reaction?
A) ${K_p} = \dfrac{{{\alpha ^2}}}{{1 + {\alpha ^2}P}}$
B) ${K_p} = \dfrac{{{\alpha ^2}{P^2}}}{{1 - {\alpha ^2}}}$
C) ${K_p} = \dfrac{{{P^2}}}{{1 - {\alpha ^2}}}$
D) ${K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}}$

Answer 1

Hint:Calculate the amount of products and reactants initially and at equilibrium. Calculate the partial pressure of both the reactants and products which is the product of mole fraction and the total pressure. Substitute these partial pressure values in the equilibrium constant formula to calculate its value.

Complete step-by-step solution:Initially, let us calculate the amount of products and reactants at $t = 0$ and at equilibrium with the given degree of dissociation as$\alpha $ . The following table shows the amount of each substance.

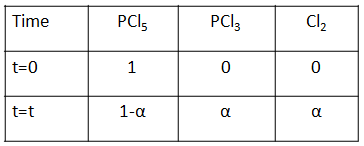
From this table, we can calculate the total number of moles as $1 - \alpha + \alpha + \alpha = 1 + \alpha $
We know that mole fraction is the number of moles of a substance divided by the total number of moles. From this we calculate the partial fraction of each substance.
${P_{PC{l_5}}} = \dfrac{{1 - \alpha }}{{1 + \alpha }}P$ , ${P_{PC{l_3}}} = \dfrac{\alpha }{{1 + \alpha }}P$ and ${P_{C{l_2}}} = \dfrac{\alpha }{{1 + \alpha }}P$
For the given reaction, the formula for equilibrium constant is ${K_p} = \dfrac{{{P_{PC{l_3}}}.{P_{C{l_2}}}}}{{{P_{PC{l_5}}}}}$
By substituting the values of partial pressure of each substance, we get ${K_p} = \dfrac{{\dfrac{{\alpha P}}{{1 + \alpha }}.\dfrac{{\alpha P}}{{1 + \alpha }}}}{{\dfrac{{1 - \alpha }}{{1 + \alpha }}P}}$
By solving this, we get ${K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}}$

Therefore, the value of equilibrium constant for the given reaction with the degree of dissociation $\alpha $ is ${K_p} = \dfrac{{{\alpha ^2}P}}{{1 - {\alpha ^2}}}$ i.e. option D.

Note: Before deriving the formula for equilibrium constant for any reaction, it is always important to balance the equation since the number of moles becomes the exponential value of the concentration or pressure. Since in this reaction, all the compounds are only one molecule, the exponential value of the partial pressures was one.