Question

In the circuit shown in figure, find the current through the branch BD.

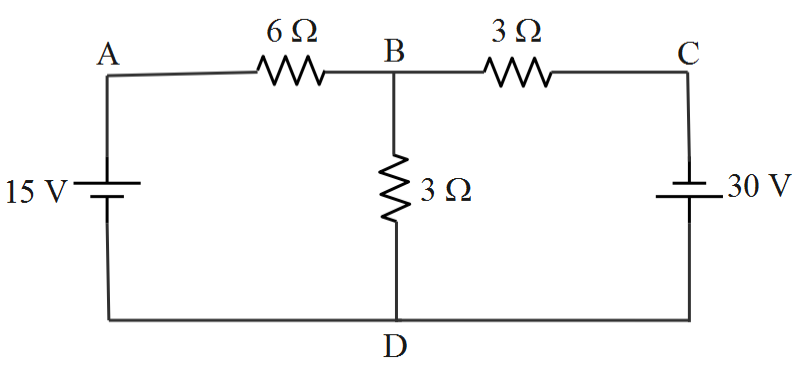
A. $5\;A$
B. $0\;A$
C. $3\;A$
D. $4\;A$

Answer 1

Hint: Use Kirchhoff’s Current Law at node B to obtain an expression for current through BD in terms of the currents due to the two supply voltages. Then, divide the circuit into two independent loops and apply Kirchhoff’s Voltage Law to each to arrive at the magnitude of currents supplied by the supply voltages. Use Ohm’s Law to find the voltage drops across the resistance elements. Then plug the values of these currents into the Current law expression to arrive at an appropriate value for current through the branch BD.

Formula Used:
Kirchhoff’s Current Law (KCL): $I_{entering} + I_{exiting} = 0$
Kirchhoff’s Voltage Law (KVL): $\Sigma V =0$
Ohm’s law: $V=IR$

Complete answer:
We employ Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL) to determine the current through the branch BD.
Kirchhoff’s Current Law (KCL) suggests that the algebraic sum of currents entering a node in a circuit will be equal to the sum of currents leaving the node.
Kirchhoff’s Voltage Law (KVL) suggests that the sum of all voltages around any closed loop in a circuit must be equal to zero.

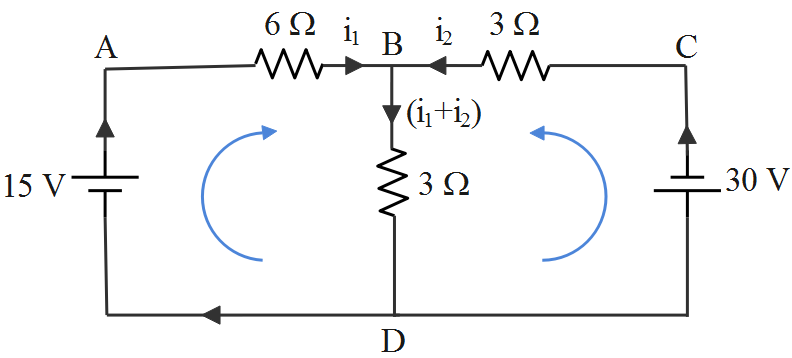
Let the current flowing through the circuit due to the $15\;V$ supply be $i_1$ and the current due to the $30\;V$ be $i_2$.
To find the current through BD, we first apply KCL at node B. We see that $i_1$ and $i_2$ flow into the node, and if $i_{BD}$ is the current through branch BD then $i_{BD}$ will flow away from the node B, i.e.,
$i_{BD} = i_1 +i_2$
Now, the voltage drops across the resistance elements can be found from Ohm’s law.
$V_{AB} = R_{AB}i_{AB} = 6i_1$
$V_{BC} = R_{BC}i_{BC} = 3i_2$
$V_{BD} = R_{BD}i_{BD} = 3(i_1+i_2)$
Now, we apply KVL to the two independent loops ABDA and BCDB deconstructed from our circuit.
For Loop ABDA:
$15-6i_1 – 3(i_1+i_2) = 0$
$\Rightarrow 15 -6i_1 -3i_1 -3i_2 = 0$
$\Rightarrow 9i_1+3i_2 = 15$ …………. (1)
For Loop BCDB:
$30 – 3i_2-3(i_1+i_2) = 0$
$\Rightarrow 30 -3i_2 -3i_1-3i_2 =0$
$\Rightarrow 3i_1+6i_2 = 30$
Multiplying the above equation by 3 we get:
$9i_1 + 18i_2 = 90$ …………… (2)
Solving (1) and (2) simultaneously we get:
$15i_2 = 75 \Rightarrow i_2 = \dfrac{75}{15} = 5\;A$
Plugging the value of $i_2$ into equation (1):
$9i_1 + 3 \times 5 = 15 \Rightarrow 9i_1 +15 = 15 \Rightarrow 9i_1=0 \Rightarrow i_1 = 0\;A$
From the KCL equation, we have:
$i_{BD} = i_1 +i_2 = 5 +0 =5A$

So, the correct answer is “Option A”.

Note: Though we looked at KCL and KVL from a quantitative perspective, it is important to understand what they mean in a physical sense.
KCL signifies conservation of charge since the law basically suggests that the sum of currents entering a node must be equal to the sum of currents leaving the node, which means that electric charges are neither ambiguously lost nor mysteriously added but remains the same in an isolated system.
KVL signifies conservation of energy since the total energy in a system remains constant, though it may be transferred between components of the system in the form of electric potential and current.