Question

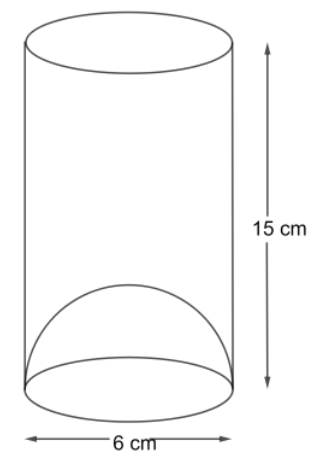
In the adjoining figure, the bottom of the glass has a hemispherical raised portion. If the glass is filled with orange juice, then the quantity of juice which a person will get is

(a) $135\pi \text{ c}{{\text{m}}^{3}}$
(b) $117\pi \text{ c}{{\text{m}}^{3}}$
(c) $99\pi \text{ c}{{\text{m}}^{3}}$
(d) $36\pi \text{ c}{{\text{m}}^{3}}$

Answer 1

Hint: The glass is a cylinder shape and there is a hemispherical raised bottom to it. We will use the formula for the volume of the cylinder and the volume of the hemisphere. We will get the volume of the glass by subtracting the volume of the hemisphere from the volume of the cylinder. The quantity of orange juice a person will get is the volume of the glass.

Complete step-by-step solution
We have a cylinder-shaped glass that has a hemispherical raised bottom. So, the volume of the glass can be calculated as
$\text{volume of glass = volume of cylinder}-\text{volume of hemisphere}$
We know that the volume of the cylinder is given by ${{V}_{C}}=\pi {{r}^{2}}h$ where $r$ is the radius of the cylinder and $h$ is the height of the cylinder. The volume of a hemisphere is given by ${{V}_{H}}=\dfrac{2}{3}\pi {{r}^{3}}$ where $r$ is the radius of the hemisphere. In this case, the radius of the cylinder and the radius of the hemisphere is the same. The diameter is given as 6 cm. So, we have a radius of 3 cm. The height of the glass, that is the cylinder, is given as 15 cm. Now, we will substitute these values and find the volume of the cylinder and the hemisphere.
The volume of the cylinder is as follows,
$\begin{align}
  & {{V}_{C}}=\pi \cdot {{\left( 3 \right)}^{2}}\cdot 15 \\
 & \Rightarrow {{V}_{C}}=\pi \times 9\times 15 \\
 & \therefore {{V}_{C}}=135\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}$
The volume of the hemisphere is as follows,
$\begin{align}
  & {{V}_{H}}=\dfrac{2}{3}\pi {{\left( 3 \right)}^{3}} \\
 & \Rightarrow {{V}_{H}}=\dfrac{2}{3}\pi \times 27 \\
 & \Rightarrow {{V}_{H}}=2\pi \times 9 \\
 & \therefore {{V}_{H}}=18\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}$
Now, we can calculate the volume of the glass in the following manner,
$\begin{align}
  & \text{volume of glass = 135}\pi -18\pi \\
 & \therefore \text{volume of glass = 117}\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}$
Hence, the correct option is (b).

Note: It is useful to know the formulae for the volumes of geometric objects in such type of questions. To avoid making errors, it is better to do the calculations explicitly. If we do not know the formula for the volume of a hemisphere, we can take the volume of the sphere having the same radius and then divide it by 2.