
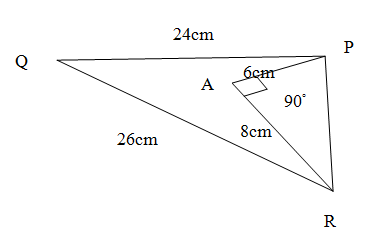
In the adjoining figure, $ PQ=24cm $, ${QR}=\text{26cm}$, $\angle PAR={{90}^{\circ }}$, PA=6cm and $ AR=8cm $. Find $\angle QPR$.

Answer
575.4k+ views
Hint: There are two triangles in the given figure $\Delta PQR$ and $\Delta PQR$. You can see one of them is right-angled. Use Pythagoras’ theorem in right angled triangles to find out the required angle.
Complete step by step answer:
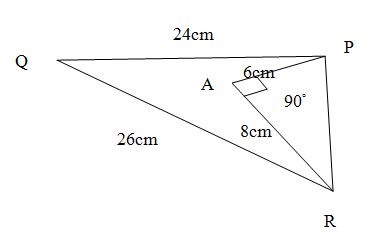
As given in the diagram there are two triangles $\Delta PQR$ and $\Delta PAR$. We can see that in $\Delta PAR$ the length of the sides as given in the question are $PA=6cm$ and $AR=8cm$ and the measurement of the angle $\angle PAR={{90}^{\circ }}$. We also see in $\Delta PQR$ , we are given the length of two sides $PQ=24cm$ and $QR=26cm$. We are asked find the measure of the angle $\angle QPR$\[\]
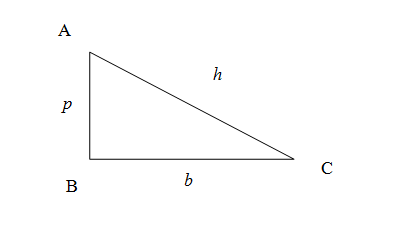
We know from the property of right angled triangles that in a right angled triangle there is a right angle otherwise known as an angle with measurement ${{90}^{\circ }}$. The side opposite to the right- angle is called hypotenuse and is denoted as $h$. Let us denote the other two sides as $p$ and $b.$ We see in the triangle we have drawn above that $\angle ABC={{90}^{\circ }},AC=h,AB=p,BC=b$\[\]
The Pythagoras theorem states that “ The triangle is right-angled if and only if the square of the hypotenuse is the sum of squares of the other two sides . ” We express it in symbols,
\[\Delta ABC\text{ is right angled }\Leftrightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
In other words,
\[\Delta ABC\text{ is right angled }\Leftrightarrow {{h}^{2}}={{p}^{2}}+{{b}^{2}}\]
Now as given in the figure $\Delta PAR$ is the right angle where $\angle PAR={{90}^{\circ }}$ is the right angle. Then its opposite side is hypotenuse $PR$ of $\Delta PAR$. Let us use Pythagoras theorem and put given values,
\[\begin{align}
& P{{R}^{2}}=P{{A}^{2}}+R{{A}^{2}}={{\left( 6cm \right)}^{2}}+{{\left( 8cm \right)}^{2}}=100c{{m}^{2}} \\
& \Rightarrow PR=\sqrt{100c{{m}^{2}}}=10cm \\
\end{align}\]
Now we shall observe $\Delta PQR$ we get, $QR=26cm$ and now $PR=10cm$. We calculate,
\[\begin{align}
& PR=10cm\Rightarrow P{{R}^{2}}=100c{{m}^{2}} \\
& PQ=24cm\Rightarrow P{{Q}^{2}}=576c{{m}^{2}} \\
& QR=26cm\Rightarrow Q{{R}^{2}}=676c{{m}^{2}} \\
\end{align}\]
We observe that $Q{{R}^{2}}=676c{{m}^{2}}=576c{{m}^{2}}+100c{{m}^{2}}=P{{Q}^{2}}+P{{R}^{2}}$. So by Pythagoas’ theorem $QR$ is the hypotenuse of the triangle $\Delta PQR$and its opposite angle $\angle QPR$ have to be right angle in other words $\angle QPR={{90}^{\circ }}$.\[\]
So, the correct answer is “${{90}^{\circ }}$”.
Note: You need to be careful substitution and use of formula in this problem. The trick here is that the statement of Pythagoras theorem is treated as a bi-conditional statement. The question can also be framed to find other acute angles but for that you need trigonometric ratios.
Complete step by step answer:

As given in the diagram there are two triangles $\Delta PQR$ and $\Delta PAR$. We can see that in $\Delta PAR$ the length of the sides as given in the question are $PA=6cm$ and $AR=8cm$ and the measurement of the angle $\angle PAR={{90}^{\circ }}$. We also see in $\Delta PQR$ , we are given the length of two sides $PQ=24cm$ and $QR=26cm$. We are asked find the measure of the angle $\angle QPR$\[\]
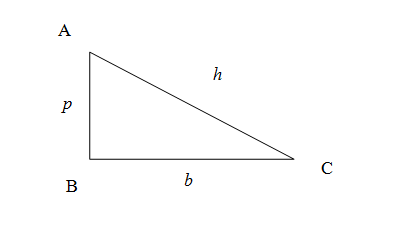
We know from the property of right angled triangles that in a right angled triangle there is a right angle otherwise known as an angle with measurement ${{90}^{\circ }}$. The side opposite to the right- angle is called hypotenuse and is denoted as $h$. Let us denote the other two sides as $p$ and $b.$ We see in the triangle we have drawn above that $\angle ABC={{90}^{\circ }},AC=h,AB=p,BC=b$\[\]
The Pythagoras theorem states that “ The triangle is right-angled if and only if the square of the hypotenuse is the sum of squares of the other two sides . ” We express it in symbols,
\[\Delta ABC\text{ is right angled }\Leftrightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
In other words,
\[\Delta ABC\text{ is right angled }\Leftrightarrow {{h}^{2}}={{p}^{2}}+{{b}^{2}}\]
Now as given in the figure $\Delta PAR$ is the right angle where $\angle PAR={{90}^{\circ }}$ is the right angle. Then its opposite side is hypotenuse $PR$ of $\Delta PAR$. Let us use Pythagoras theorem and put given values,
\[\begin{align}
& P{{R}^{2}}=P{{A}^{2}}+R{{A}^{2}}={{\left( 6cm \right)}^{2}}+{{\left( 8cm \right)}^{2}}=100c{{m}^{2}} \\
& \Rightarrow PR=\sqrt{100c{{m}^{2}}}=10cm \\
\end{align}\]
Now we shall observe $\Delta PQR$ we get, $QR=26cm$ and now $PR=10cm$. We calculate,
\[\begin{align}
& PR=10cm\Rightarrow P{{R}^{2}}=100c{{m}^{2}} \\
& PQ=24cm\Rightarrow P{{Q}^{2}}=576c{{m}^{2}} \\
& QR=26cm\Rightarrow Q{{R}^{2}}=676c{{m}^{2}} \\
\end{align}\]
We observe that $Q{{R}^{2}}=676c{{m}^{2}}=576c{{m}^{2}}+100c{{m}^{2}}=P{{Q}^{2}}+P{{R}^{2}}$. So by Pythagoas’ theorem $QR$ is the hypotenuse of the triangle $\Delta PQR$and its opposite angle $\angle QPR$ have to be right angle in other words $\angle QPR={{90}^{\circ }}$.\[\]
So, the correct answer is “${{90}^{\circ }}$”.
Note: You need to be careful substitution and use of formula in this problem. The trick here is that the statement of Pythagoras theorem is treated as a bi-conditional statement. The question can also be framed to find other acute angles but for that you need trigonometric ratios.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




