Question

In the adjoining diagram, the condenser C will be fully charged to potential V if :

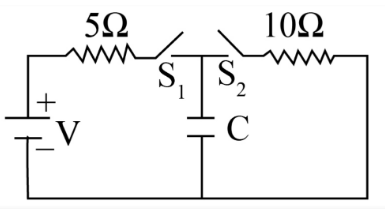
A. \[{S_1}\] and \[{S_2}\] both are open
B. \[{S_1}\] and \[{S_2}\] both are closed
C. \[{S_1}\] is closed and \[{S_2}\] is open
D. \[{S_1}\] is open and \[{S_2}\] is closed

Answer 1

Hint: The above problem can be resolved using the introductory circuit analysis techniques and some fundamental rules to resolve the complex circuit, namely Kirchhoff’s Voltage rule or simply KVL. The different cases are undertaken to consider the current flow and the corresponding value of the potential difference across C. At last, the appropriate combination is to be undertaken to obtain the conclusion.

Complete step by step answer:
Consider the first case, when the switches are closed.
Let I be the current through the circuit and apply the KVL rule as,
\[
 - V + 5\;\Omega \times I + 10\;\Omega \times I = 0\\
\Rightarrow I = \dfrac{V}{{15}}\;{\rm{A}}
\]
And the potential difference across C is,
\[
V = 5\;\Omega \times I - 10\;\Omega \times I\\
\Rightarrow V = 5\;\Omega \times \left( {\dfrac{V}{{15}}} \right)\;{\rm{A}} - 10\;\Omega \times \left( {\dfrac{V}{{15}}} \right)\;{\rm{A}}\\
\Rightarrow V = - \dfrac{V}{3}
\]
-Now, consider the second case, when both the switches are open. In this case, the circuit is not completed and the charge flow through the capacitor is zero. Therefore, the potential difference across C is zero.
-Consider the third case, where \[{S_1}\] is closed and \[{S_2}\] is open.In this case, the flow of current in equilibrium is zero, but the potential difference is V across the capacitor.
-Consider the fourth case, where \[{S_1}\] is open and \[{S_2}\] is closed.In this case, the battery is not connected with the circuit, hence there is no power source to alter the reading of the capacitor.

Therefore, the condenser C will be fully charged to potential V if \[{S_1}\] is closed and \[{S_2}\] is open and option ( C ) is correct.

Note: Try to understand the various methods to resolve the complex circuits and obtain the relationship for current and voltages' corresponding magnitude. Moreover, conditions for the zero potential are also needed to take under consideration to resolve such problems.