Question

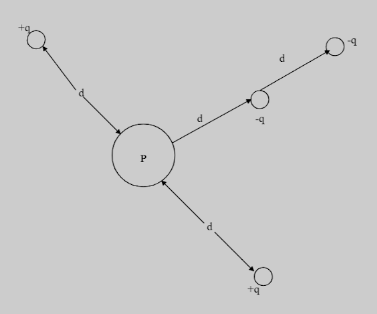
In the above figure, what is the net electric potential at point P due to the four particles if $ V = 0 $ at infinity, $ q = 5.00fC $ and $ d = 4.00cm $ ?

Answer 1

Hint: Electric field is a vector quantity, while electric potential is a scalar quantity. Thus, to find the electric potential on a point due to several other point charges, we could make a sum of their individual electric potential with respect to the point charge. So, to find the electric potential on point P due to the other point charges, we can find the electric potential of each point charge on P and add them, $ V = {V_1} + {V_2} + {V_3} + {V_4} $ .

Formulas used We will be using the formula to find the electric potential of a point charge on a body given by, $ V = \dfrac{{kq}}{d} $ , where $ V $ is the electric potential on a point by a point charge, $ q $ is the magnitude of the point charge, $ d $ is the distance between the charge and the point, and $ k $ is the electrostatic constant given by, $ k = \dfrac{1}{{4\pi {\varepsilon _0}}} $ .

Complete Step by Step Solution
We can see that there are 4 charges surrounding the point P, in 3 directions. There are 2 point charges $ + q $ at a distance $ d $ in two opposite sides of point P, and a charge $ - q $ at a distance $ 2d $ from P, and another charge $ - q $ at a distance $ d $ from the point P in the same direction along the previously mentioned charge.
The electric potential of charges at either side of point P on P are given by,
 $ {V_1} = {V_2} = \dfrac{{k( + q)}}{d} $
Similarly, the electric potential on point P, due to the third charge,
 $ {V_3} = \dfrac{{k( - q)}}{{2d}} $
And the electric potential on point P due to the fourth charge will be,
 $ {V_4} = \dfrac{{k( - q)}}{d} $
We know that electric potential is a scalar quantity, thus the total electric potential on point P is simply the sum of all the electric potentials on point P, $ V = {V_1} + {V_2} + {V_3} + {V_4} $ .
 $ {V_{total}} = \dfrac{{k( + q)}}{d} + \dfrac{{k( + q)}}{d} + \dfrac{{k( - q)}}{{2d}} + \dfrac{{k( - q)}}{d} $
 $ {V_{total}} = kq\left[ {\dfrac{{( + 1)}}{d} + \dfrac{{( + 1)}}{d} + \dfrac{{( - 1)}}{{2d}} + \dfrac{{( - 1)}}{d}} \right] $
Substituting the value of $ k = \dfrac{1}{{4\pi {\varepsilon _0}}} $ and solving,
 $ {V_{total}} = \dfrac{1}{{4\pi {\varepsilon _0}}}q\left[ {\dfrac{{(2 + 2 - 1 - 2)}}{{2d}}} \right] $
 $ {V_{total}} = \dfrac{1}{{4\pi {\varepsilon _0}}}q\left[ {\dfrac{{(1)}}{{2d}}} \right] $
We also know that the $ q = 5.00fC = 5 \times {10^{ - 15}}C $ , $ d = 4.00cm = 4 \times {10^{ - 2}}m $ and the value of the electrostatic constant, $ k = \dfrac{1}{{4\pi {\varepsilon _0}}} = 8.996 \times {10^9}N{m^2}{C^{ - 2}} $ .
 $ {V_{total}} = 8.996 \times {10^9}N{m^2}{C^{ - 2}} \times 5 \times {10^{ - 15}}C\left[ {\dfrac{{(1)}}{{2 \times 4 \times {{10}^{ - 2}}m}}} \right] $
Solving for $ {V_{total}} $ we get,
 $ {V_{total}} = 5.5625 \times {10^{ - 4}}Nm/C $ .

Note
The electric potential is a scalar quantity because it is a ratio of the potential energy of the system per unit charge, but the electric field is a vector because it is the ratio of the electric force applied to the distance.