Question

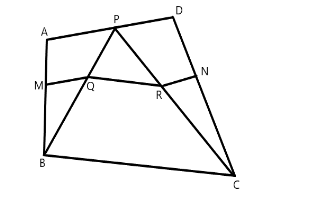
In quadrilateral ABCD, M is o $ \overline {AB} $ and N is o $ \overline {DC} $ such that $ \dfrac{{AM}}{{MB}} = \dfrac{{DN}}{{NC}} $ . P is any pointy on $ \overline {AD} $ . Line parallel to $ \overline {AD} $ through M intersects $ \overline {BP} $ at Q and through N intersects $ \overline {CP} $ at R. Prove that $ \overline {QR} \parallel \overline {BC} $ .
 

Answer 1

Hint: Two objects are similar if they have the same shape, they can have different sizes and orientations. There are several ways to prove two triangles similar, some of them are AA similarity criterion, SAS similarity criterion, and SSS similarity criterion. Use a suitable way to prove some triangles similar to each other in the given question to reach the required result.

Complete step-by-step answer:
We are given that line parallel to AD intersects BP at Q that is $ MQ\parallel AP $ .
We know that corresponding angles of parallel lines are always equal so
 $ \angle BQM = \angle BPA $ and $ \angle BMQ = \angle BAP $ . Also $ \angle ABP $ is common in both the triangles.
So by AAA similarity criterion, $ \vartriangle ABP \sim \vartriangle MBQ $
As the triangles are similar, we can say that $ \dfrac{{AB}}{{MB}} = \dfrac{{BP}}{{BQ}} = \dfrac{{AP}}{{MQ}} $
We are also given that the line parallel to AD intersects PC at N that is $ NR\parallel AD $
We know that corresponding angles of parallel lines are always equal so
\[\angle CNR = \angle CDP\] and $ \angle CRN = \angle CPD $ . Also $ \angle PCD $ is common in both the triangles.
So by AAA similarity criterion $ \vartriangle PCD \sim \vartriangle RCN $
As the triangles are similar, we can say that $ \dfrac{{PC}}{{RC}} = \dfrac{{CD}}{{CN}} = \dfrac{{PD}}{{RN}} $
Now we are given in the question that $ \dfrac{{AM}}{{MB}} = \dfrac{{DN}}{{NC}} $
Adding 1 on both sides, we get –
 $
  \dfrac{{AM}}{{MB}} + 1 = \dfrac{{DN}}{{NC}} + 1 \\
  \dfrac{{AB}}{{MB}} = \dfrac{{DC}}{{NC}} \\
  $
Using the above relation and the similarity of triangles, we observe that
 $
  \dfrac{{AB}}{{MB}} = \dfrac{{BP}}{{BQ}} = \dfrac{{AP}}{{MQ}} = \dfrac{{PC}}{{RC}} = \dfrac{{CD}}{{CN}} = \dfrac{{PD}}{{RN}} \\
   \Rightarrow \dfrac{{BP}}{{BQ}} = \dfrac{{CP}}{{CR}} \\
   \Rightarrow \dfrac{{BQ}}{{BP}} = \dfrac{{CP}}{{CR}} \\
  $
Subtracting 1 from both sides, we get –
 $
  \dfrac{{BQ}}{{BP}} - 1 = \dfrac{{CR}}{{CP}} - 1 \\
  \dfrac{{ - (BP - BQ)}}{{BP}} = \dfrac{{ - (CP - CR)}}{{CP}} \\
  \dfrac{{QP}}{{BP}} = \dfrac{{RP}}{{CP}} \\
  $
 $ \angle BPC $ is common in both the triangles.
So by SAS criterion, $ \vartriangle BPC \sim \vartriangle QPR $
As the two triangles are similar, we have $ \angle B = \angle Q $ and $ \angle C = \angle R $
They form two pairs of corresponding angles, thus line QR is parallel to BC.
Hence proved, $ \overline {QR} \parallel \overline {BC} $
So, the correct answer is “$ \overline {QR} \parallel \overline {BC} $ ”.

Note: If two sides of a triangle are in the same proportion as the two sides of another triangle, and the angle inscribed by the two sides in both the triangles are equal, then the triangles are said to be similar. If any two or more angles of a triangle are equal to any two or more angles of another triangle, then the two triangles are said to be similar.