Question

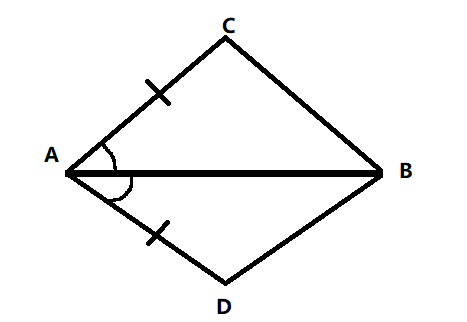
In quadrilateral ABCD, AC=AD and AB bisects $\angle CAD$. Show that $\vartriangle {\text{ABC}} \cong \vartriangle {\text{ABD}}$. What can you say about BC and BD?

Answer 1

Hint: We will use given conditions to show that the two sides and angle between the sides are equal of the triangles $\vartriangle {\text{ABC}}$ and $\vartriangle {\text{ABD}}$. We will then prove $\vartriangle {\text{ABC}}$ and $\vartriangle {\text{ABD}}$congruent using SAS (side-angle-side) property of congruency. At last, we will use the CPCT property of congruent triangles to tell about the relation between BC and BD.

Complete step by step Answer:

We are given that AC=AD and AB bisect $\angle CAD$.

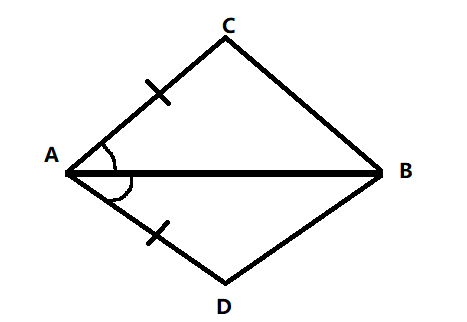
Since, AB bisects $\angle CAD$, it divides the corresponding angle in two equal parts. That is,
$\angle CAB = \angle DAB$
We have to prove that $\vartriangle {\text{ABC}} \cong \vartriangle {\text{ABD}}$
Consider triangles $\vartriangle {\text{ABC}} \cong \vartriangle {\text{ABD}}$
We are already given that AC=AD
Since, AB bisects $\angle CAD$, we have $\angle CAB = \angle DAB$
Also, AB is common in both the triangles.
Then, we use side-angle-side (SAS) criterion to prove $\vartriangle {\text{ABC}} \cong \vartriangle {\text{ABD}}$
Hence, $\vartriangle {\text{ABC}} \cong \vartriangle {\text{ABD}}$
Now, corresponding parts of congruent triangles will be equal.
Hence, ${\text{BC = BD}}$

Note: While applying the congruency rule, side-angle-side, the corresponding sides and the angle between the sides should be equal. One must be careful while selecting the angle for the side-angle-side congruency rule. Also, students must know the rules of congruency for these types of questions.