Question

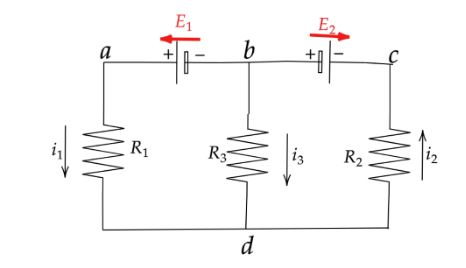
In Figure, what is the potential difference ${V_d} - {V_c}$ between point d and c if ${E_1} = 0.4V$, ${E_2} = 1.0V$ ,${R_1} = {R_2} = 10\Omega $, and ${R_3} = 5.0\Omega $, and the battery is ideal.

Answer 1

Hint: Here we have to find the potential difference between the two terminals d and c. First we will find the values of their difference current in diffract branches of the circuit using the given information. Then after taking two different paths one is branch d to b to c and the other one is d to c hence from that we will get two same potential difference values for both the way.

Complete step by step answer:
As per the given problem we have a figure where ${E_1} = 4.0V$, ${E_2} = 1.0V$ ,${R_1} = {R_2} = 10\Omega $, and ${R_3} = 5.0\Omega $, and the battery is ideal.Now we need to calculate the value of potential difference ${V_d} - {V_c}$ between point d and c.Now from the above given figure we can write,
${i_1} = \dfrac{{{E_1}\left( {{R_2} + {R_3}} \right) - {E_2}{R_3}}}{{{R_1}{R_2} + {R_2}{R_3} + {R_1}{R_3}}}$
We know,
${E_1} = 4.0V$
$\Rightarrow {E_2} = 1.0V$
$\Rightarrow {R_1} = {R_2} = 10\Omega $
$\Rightarrow {R_3} = 5.0\Omega $

Now putting the given values we will get,
${i_1} = \dfrac{{\left( {4.0V} \right)\left( {10\Omega + 5\Omega } \right) - \left( {1.0V} \right)\left( {5\Omega } \right)}}{{\left( {10\Omega } \right)\left( {10\Omega } \right) + \left( {10\Omega } \right)\left( {5\Omega } \right) + \left( {10\Omega } \right)\left( {5\Omega } \right)}}$
On further solving and simplifying we will get,
${i_1} = 0.275A$
Similarly from the figure we can write,
${i_2} = \dfrac{{{E_1}{R_3} - {E_2}\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2} + {R_2}{R_3} + {R_1}{R_3}}}$
We know,
${E_1} = 4.0V$
$\Rightarrow {E_2} = 1.0V$
$\Rightarrow {R_1} = {R_2} = 10\Omega $
$\Rightarrow {R_3} = 5.0\Omega $

Now putting the given values we will get,
${i_2} = \dfrac{{\left( {4.0V} \right)\left( {5\Omega } \right) - \left( {1.0V} \right)\left( {10\Omega + 5\Omega } \right)}}{{\left( {10\Omega } \right)\left( {10\Omega } \right) + \left( {10\Omega } \right)\left( {5\Omega } \right) + \left( {10\Omega } \right)\left( {5\Omega } \right)}}$
On further solving and simplifying we will get,
${i_2} = 0.025A$
Now from the figure we can write,
${i_3} = {i_2} - {i_1} = 0.025A - 0.275A = - 0.250A$
Now to find the potential differ,
We can two different oath two calculate the potential difference

Case I:From point d to b to c we will get,
${V_d} + {i_3}{R_3} + {E_2} = {V_c}$
We know,
${i_3} = - 0.250A$
$\Rightarrow {R_3} = 5.0\Omega $
$\Rightarrow {E_2} = 1.0V$
Now putting the known value we will get,
${V_d} + \left( { - 0.250A} \right)\left( {5\Omega } \right) + 1.0V = {V_c}$
On soling we will get,
${V_d} - 0.250V = {V_c}$
On rearranging we will get,
${V_d} - {V_c} = 0.250V$

Case II: From point d to c we will get,
${V_d} - {i_2}{R_2} = {V_c}$
We know,
${i_2} = 0.025A$
$\Rightarrow {R_2} = 10\Omega $
Now putting the known value we will get,
${V_d} - \left( {0.025A} \right)\left( {10\Omega } \right) = {V_c}$
On soling we will get,
${V_d} - 0.250V = {V_c}$
On rearranging we will get,
$\therefore {V_d} - {V_c} = 0.250V$

Hence,the potential difference ${V_d} - {V_c}$ between point d and c is 0.250 V.

Note: Remember that potential difference is the difference in the amount of energy that a charge carrier has between two points in a circuit as in this equation the two points are d and c. Note that whatever the path the current has travelled, the potential difference between that point will always remain the same and it is measured in terms of voltage.