Question

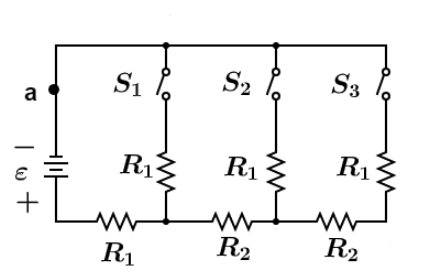
In Figure. ${R_1} = 20\Omega $ , ${R_2} = 10\Omega $ and the ideal battery has emf $\varepsilon = 120V$ what is the current at point “a” if we close (a) only switch ${S_1}$ (b) only switches ${S_1}$ and ${S_2}$ (c) all three switches?

Answer 1

Hint: In order to solve this question we need to understand the electrical circuits and Kirchhoff’s law. So electrical circuits are defined as circuits containing electrical equipment like resistor, capacitor etc. Switches are used in circuits so that we can have a control over current flow in the circuit. There are two laws of Kirchhoff, one is junction law and other is closed loop law. According to junction law, there would be no accumulation of charges at the junction, so the amount of current entering the junction must leave the junction by the same amount. Kirchhoff closed loop law, indicates that potential around a closed loop is always zero.

Complete step by step answer:
First of all we have to indicate arms, so we name junction points as shown in figure.

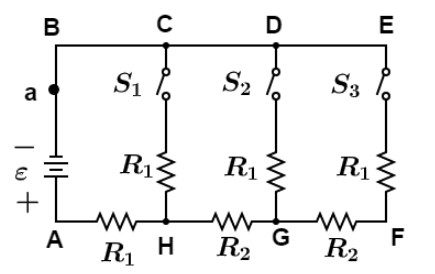
Case $a$ When only switch ${S_1}$ is closed. Since switches ${S_2}\& {S_3}$ are open, there would be no current in arm DG and EF. Hence we can remove these arms and the final circuit would look like as shown in figure.

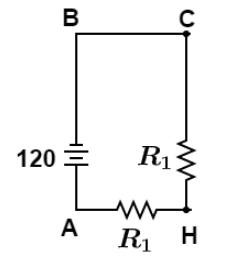
Let current $i$ flown in circuit. So the current through point “a” is $i$ remember, since point a indicated in the given question figure lies in arm AB so current through point a will always be the same as current I flowing in arm AB for all three different cases.
Applying Kirchhoff law in loop ABCHA we get,
$ - 120 + i{R_1} + i{R_1} = 0$
$\Rightarrow i = \dfrac{{120}}{{2{R_1}}}$
$\Rightarrow i = \dfrac{{60}}{{{R_1}}}$
Putting values we get,
$i = \dfrac{{60}}{{20}}$
$\Rightarrow i = 3\,A$

So current through point “a” is $3A$.

Case $b$ when both switches ${S_1}\& {S_2}$ are closed.Since switches ${S_3}$ are open, so there would be no current in arm EF. Hence we can remove this arm and the final circuit would look like as shown in figure.

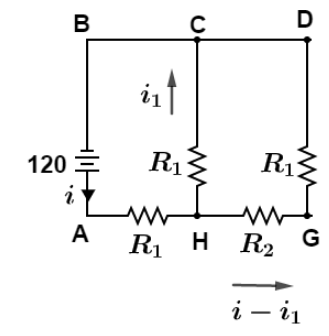
We would distribute the current as shown in figure
Applying Kirchhoff law in loop ABCHA we get,
\[ - 120 + i{R_1} + {i_1}{R_1} = 0\]
\[\Rightarrow i + {i_1} = \dfrac{{120}}{{{R_1}}}\]
Putting values we get,
\[i + {i_1} = \dfrac{{120}}{{20}}\]
\[\Rightarrow i + {i_1} = 6 \to (i)\]
Now applying Kirchhoff law in loop HGDGH we get,
$(i - {i_1}){R_2} + (i - {i_1}){R_1} - {i_1}{R_1} = 0$
$\Rightarrow i({R_1} + {R_2}) - {i_1}({R_2} + 2{R_1}) = 0$
Putting values we get,
$i(20 + 10) - {i_1}(10 + 40) = 0$
$\Rightarrow 30i - 50{i_1} = 0$
$\Rightarrow {i_1} = \dfrac{5}{3}i$
Putting value of ${i_1}$ in equation (i) we get,
$i + \dfrac{5}{3}i = 6$
$\Rightarrow \dfrac{8}{3}i = 6$
$\Rightarrow i = \dfrac{{6 \times 3}}{8}$
$\Rightarrow i = \dfrac{{15}}{4}A$

So the current through point “a” is, $\dfrac{{15}}{4}A$.

Case $c$ when all switches are closed. We would distribute the current as shown in figure,

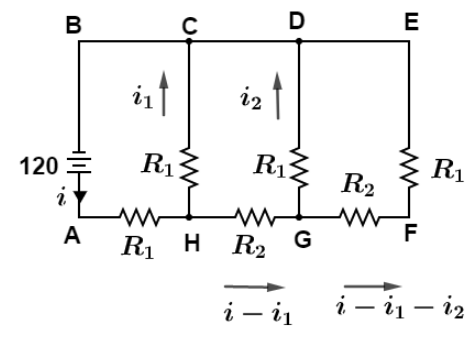
Applying Kirchhoff’s law in ABCDH we get,
\[ - 120 + i{R_1} + {i_1}{R_1} = 0\]
\[\Rightarrow i + {i_1} = \dfrac{{120}}{{{R_1}}}\]
Putting values we get,
\[i + {i_1} = \dfrac{{120}}{{20}}\]
\[\Rightarrow i + {i_1} = 6 \to (i)\]
Applying Kirchhoff’s law in HGDCH we get,
$(i - {i_1}){R_2} + {i_2}{R_1} - {i_1}{R_1} = 0$
$\Rightarrow i{R_2} - {i_1}({R_1} + {R_2}) + {i_2}({R_1}) = 0$
Putting values we get, $10i - 30{i_1} + 20{i_2} = 0$
$i - 3{i_1} + 2{i_2} = 0 \to (ii)$
Applying Kirchhoff’s law in loop GFEDG we get,
$(i - {i_1} - {i_2}){R_2} + (i - {i_1} - {i_2}){R_1} - {i_2}{R_1} = 0$
$\Rightarrow i({R_1} + {R_2}) - {i_1}({R_1} + {R_2}) - {i_2}({R_2} + 2{R_1}) = 0$

Putting values we get,
$30i - 30{i_1} - 50{i_2} = 0$
$\Rightarrow 3i - 3{i_1} - 5{i_2} = 0 \to (iii)$
Now doing operation $E{q^n}(ii) \times 5 + E{q^n}(iii) \times 2$ we get,
$5(i - 3{i_1} + 2{i_2}) + 2(3i - 3{i_1} - 5{i_2}) = 0$
$\Rightarrow 11i - 9{i_1} = 0 \to (iv)$
Again doing operation we get, $E{q^n}(i) \times 9 + E{q^n}(iv)$ we get,
$9(i + {i_1}) + 11i - 9{i_1} = 9 \times 6$
$\Rightarrow 11i + 9i = 54$
$\Rightarrow 20i = 54$
$\Rightarrow i = \dfrac{{54}}{{20}}$
$\Rightarrow i = \dfrac{{27}}{{10}}$
$\therefore i = 2.7\,A$

So current through point “a” is, $2.7\,A$.

Note: It should be remembered that, we have used here Kirchhoff rule of potential to first form the equation and later we solve those equations, this type of analysis is known as mesh analysis, where each loop is called mesh. However we can also solve this question by nodal analysis, where we assume potential of each junction and later solve those.