
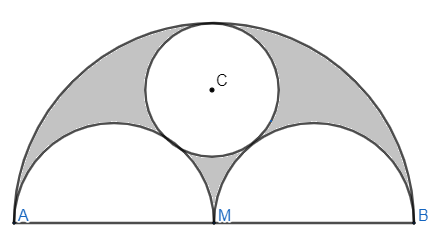
In figure \[AB=36cm\] and M is the mid-point of AB. Semicircles are drawn on AB. AM and MB as diameter. A circle with centre C touches all the three circles. Find the area of the shaded region.

Answer
507.9k+ views
Hint: We are given a semicircle with two semicircles and a circle inside. We are given certain measurements of their radii. And we are asked to find the area of the shaded region as can be seen in the above given figure. The radii of the two semicircles inside the bigger semicircle is so their area can be calculated using the formula \[\dfrac{1}{2}\pi {{r}^{2}}\]. But the radius of the circle inside the semicircle is not known. So, we will find the radius of the circle and then we will have the area of the circle as well. Then, in order to find the area of the shaded region, we will subtract the area of two smaller semicircles and the circle from the area of the bigger semicircle. Hence, we will have the area of the shaded region.
Complete step by step answer:
According to the given question, we are given a semicircle with two semicircles and a circle inside. We are given the diameter of the outer semicircle also. We are asked to find the area of the shaded region as can be seen in the given figure.
We are given that, \[AB=36cm\]
And that M is the mid-point of AB, so that means, we have,
\[AM=MB=18cm\]
Let there be another point P and Q which are the mid-points of AM and MB respectively.
So, we get,
\[AP=PM=MQ=QB=9cm\]
But we still don’t know the radius of the circle.
Let the radius of the circle be ‘r’ and now we join the centre of the circle C to P and Q. Also, a line passing through M and the centre of circle C to meet the circumference of the outer semicircle at the point R.
So, we have the figure as below,
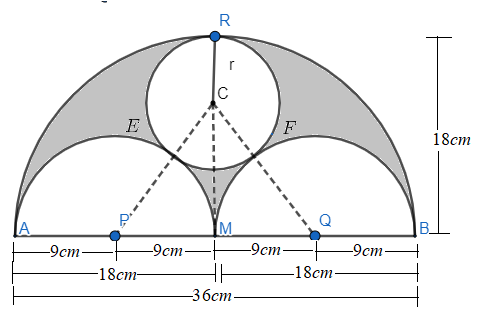
We have, \[RC=r\]
So, we get, \[CM=18-r\] and \[PC=9+r\]
Now, we will consider the right triangle \[\vartriangle CMP\],
\[P{{C}^{2}}=C{{M}^{2}}+M{{P}^{2}}\] (Using Pythagoras theorem)
Substituting the known values, we get,
\[\Rightarrow {{\left( 9+r \right)}^{2}}={{\left( 18-r \right)}^{2}}+{{9}^{2}}\]
\[\Rightarrow 81+{{r}^{2}}+18r=324+{{r}^{2}}-36r+81\]
\[\Rightarrow 18r=324-36r\]
\[\Rightarrow 54r=324\]
\[\Rightarrow r=6cm\]
Now, we will find the area of the shaded region, we have,
Area of the shaded region = Area of the semicircle with mid-point M – (Area of semicircle with P as the mid-point + Area of the semicircle with Q as the mid-point + Area of the circle with C as the centre)
\[\Rightarrow \dfrac{1}{2}\pi {{\left( AM \right)}^{2}}-\dfrac{1}{2}\pi {{\left( AP \right)}^{2}}-\dfrac{1}{2}\pi {{\left( QB \right)}^{2}}-\pi {{\left( CR \right)}^{2}}\]
We will substitute the values and we get,
\[\Rightarrow \dfrac{1}{2}\pi {{(18)}^{2}}-\dfrac{1}{2}\pi {{(9)}^{2}}-\dfrac{1}{2}\pi {{(9)}^{2}}-\pi {{(6)}^{2}}\]
\[\Rightarrow \dfrac{1}{2}324\pi -\dfrac{1}{2}81\pi -\dfrac{1}{2}81\pi -36\pi \]
\[\Rightarrow 162\pi -81\pi -36\pi \]
\[\Rightarrow 45\pi c{{m}^{2}}\]
Therefore, the area of the shaded region is \[45\pi c{{m}^{2}}\].
Note: The area of the shaded region refers to those regions which are coloured in the given figure. Do not interpret it otherwise. Also, the calculations are lengthy so it is advised to carry out the calculation step – wise. Also, the area of a semicircle is half the area of the circle as a semicircle is half of a circle.
Complete step by step answer:
According to the given question, we are given a semicircle with two semicircles and a circle inside. We are given the diameter of the outer semicircle also. We are asked to find the area of the shaded region as can be seen in the given figure.
We are given that, \[AB=36cm\]
And that M is the mid-point of AB, so that means, we have,
\[AM=MB=18cm\]
Let there be another point P and Q which are the mid-points of AM and MB respectively.
So, we get,
\[AP=PM=MQ=QB=9cm\]
But we still don’t know the radius of the circle.
Let the radius of the circle be ‘r’ and now we join the centre of the circle C to P and Q. Also, a line passing through M and the centre of circle C to meet the circumference of the outer semicircle at the point R.
So, we have the figure as below,

We have, \[RC=r\]
So, we get, \[CM=18-r\] and \[PC=9+r\]
Now, we will consider the right triangle \[\vartriangle CMP\],
\[P{{C}^{2}}=C{{M}^{2}}+M{{P}^{2}}\] (Using Pythagoras theorem)
Substituting the known values, we get,
\[\Rightarrow {{\left( 9+r \right)}^{2}}={{\left( 18-r \right)}^{2}}+{{9}^{2}}\]
\[\Rightarrow 81+{{r}^{2}}+18r=324+{{r}^{2}}-36r+81\]
\[\Rightarrow 18r=324-36r\]
\[\Rightarrow 54r=324\]
\[\Rightarrow r=6cm\]
Now, we will find the area of the shaded region, we have,
Area of the shaded region = Area of the semicircle with mid-point M – (Area of semicircle with P as the mid-point + Area of the semicircle with Q as the mid-point + Area of the circle with C as the centre)
\[\Rightarrow \dfrac{1}{2}\pi {{\left( AM \right)}^{2}}-\dfrac{1}{2}\pi {{\left( AP \right)}^{2}}-\dfrac{1}{2}\pi {{\left( QB \right)}^{2}}-\pi {{\left( CR \right)}^{2}}\]
We will substitute the values and we get,
\[\Rightarrow \dfrac{1}{2}\pi {{(18)}^{2}}-\dfrac{1}{2}\pi {{(9)}^{2}}-\dfrac{1}{2}\pi {{(9)}^{2}}-\pi {{(6)}^{2}}\]
\[\Rightarrow \dfrac{1}{2}324\pi -\dfrac{1}{2}81\pi -\dfrac{1}{2}81\pi -36\pi \]
\[\Rightarrow 162\pi -81\pi -36\pi \]
\[\Rightarrow 45\pi c{{m}^{2}}\]
Therefore, the area of the shaded region is \[45\pi c{{m}^{2}}\].
Note: The area of the shaded region refers to those regions which are coloured in the given figure. Do not interpret it otherwise. Also, the calculations are lengthy so it is advised to carry out the calculation step – wise. Also, the area of a semicircle is half the area of the circle as a semicircle is half of a circle.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Which of the following does not have a fundamental class 10 physics CBSE

10 examples of evaporation in daily life with explanations

State and prove the Pythagoras theorem-class-10-maths-CBSE

State BPT theorem and prove it class 10 maths CBSE

What is UltraEdge (Snickometer) used for in cricket?

What are the public facilities provided by the government? Also explain each facility




