Question

In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.

Answer 1

Hint: Here, in a triangle, the point which is equal distance from all three sides of the triangle is placed at the bisector of all angles inside the triangle.

The following is the schematic diagram of triangle ABC.

Complete step-by-step solution
Given, a triangle $\Delta ABC$

1. First draw an arc of any radius intersecting side AB and AC at point E and D respectively.
2. Next draw arcs from D and E with the same radius intersecting each other, mark the point as F. join F with point A.
3. It is the bisector of $\angle A$.
4. Similarly draw bisectors of$\angle B\,{\rm{and}}\,\angle {\rm{C}}$.
5. Extend the bisectors until they meet at one point. This intersection point is the triangle which is placed at equidistant from all sides.

Therefore, O is the point which is equidistant from all the sides of the triangle.
                                                

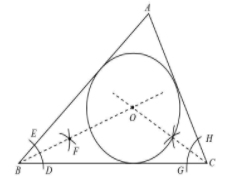
Note:While drawing bisectors remembering that radius of compass should be the same from point D and E. If there is a difference in radius, then we cannot draw the correct bisector of an angle A.