Question

In a small village of Jharkhand, panjunia (name of the village), there was a blacksmith. He made different types of \[3D\] solid shapes. One day he got an order from Ramu for making of $14cm$ long cylindrical rods of \[2cm\] radius. He had solid iron boxes whose dimensions were \[20cm \times 16cm \times 11cm\].How many rods Ramu will get from one solid box.

Answer 1

Hint: Similar geometry types of questions we explore are listed in the scenario of the given problem to determine the definition of the property and replace the given value in the geometric form, we get the correct solution of the given problem and to using the specific formula for evaluate the answer.

Formula Used:
Cylindrical rod formula,
$V = Bh$ or $V = \pi {r^2}h$
Where,
$V$ represent as Volume, $B$ represent as Base, $h$ represent as Height, and \[r\] represent as Radius
Cylinder,
Flat Surface $ = 2$ Curved Surface $ = 1$ Face \[ = 3\] Edges $ = 2$ Vertices \[ = 0\]
Surface Area Formula (Square Units) $2\pi r\left( {r + h} \right)$
$volume\,of\,cuboid = lbh$
Where, length $l$, breath \[b\], height \[h\]

Complete step-by-step answer:
Given by,
Height of the cylindrical rod is \[14\]$cm$
Radius of the cylindrical rod is $2cm$
Solid iron box dimension,
Length is $20cm$
Breath is \[16cm\]
Height is $11cm$
Cylindrical rod is $2\pi r\left( {r + h} \right)$

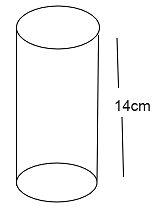
Substituting a given value in the above equation,
We get,
Cylindrical rod $ = 2 \times \dfrac{{24}}{7} \times 2\left( {2 + 14} \right)$
Simplified as,
$ = 2 \times \dfrac{{24}}{7} \times 2\left( {16} \right)\,c{m^2}$
Volume of Cuboid $ = lbh$
Substituting the given values,
Here,

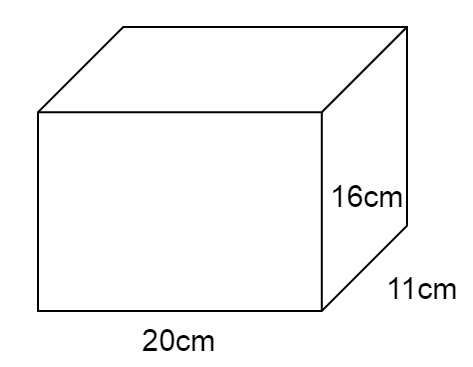
We get,
Volume of the cuboid $ = 20cm \times 16cm \times 11cm$
Number of cylindrical rods obtained by the iron box$ = \dfrac{{volume\,of\,cuboid}}{{cylindrical\,rod}}$
$ = \dfrac{{20cm \times 16cm \times 11cm}}{{2 \times \dfrac{{22}}{7} \times 2 \times 16}}$
Simplified above equation,
We get,
$17rods\,$
Hence the number of cylindrical rods obtained by the iron box is $17$ rods.

Note: In this above problem, the established concept of geometric in this statement gives an example of the cylindrical rod and solid so that we can easily analyze the number of rods. we used to apply the formula of one cylindrical rod and the value gets a decimal point so that we obtain the value of the rods.