Question

In a series RC circuit, $R = 500\Omega $, $C = 2\mu F$, $V = 282\sin (377t)$. The power consumed
A. $14100W$
B. $141W$
C. $10W$
D. $14.1W$

Answer 1

Hint: In the RC circuit, they’ve given the values of resistance, capacitance and ac voltage of the circuit. To find the power consumed by this circuit, we need to know the rms values of current and voltage and the power factor. In order to know these values, we need to find the impedance of the circuit.
Formula used:
$\eqalign{
  & Z = \sqrt {{R^2} + {X_C}^2} \cr
  & {X_C} = \dfrac{1}{{\omega C}} \cr
  & {i_0} = \dfrac{{{V_0}}}{Z} \cr
  & \cos \phi = \dfrac{R}{Z} \cr
  & P = {i_{rms}}{V_{rms}}\cos \phi \cr} $

Complete answer:
In the problem, they’ve given an RC circuit, with a resistor $R = 500\Omega $ and capacitor $C = 2\mu F$. An ac voltage source of $V = {V_0}\sin \left( {\omega t} \right) = 282\sin (377t)$ is also given.

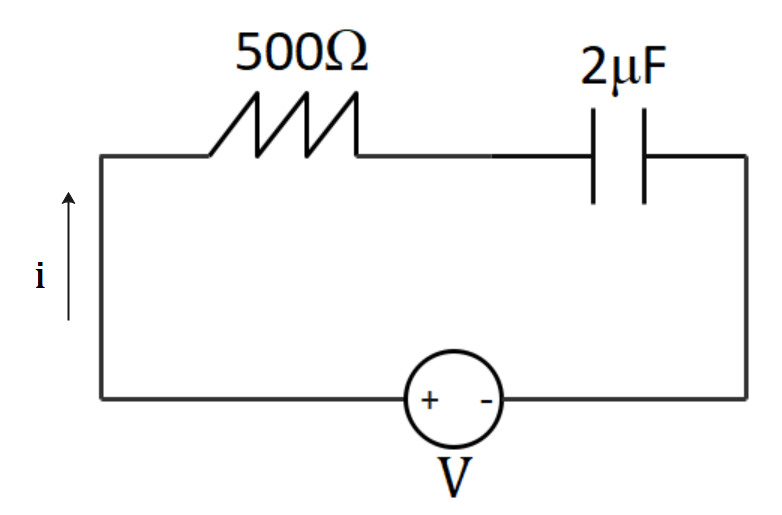
The total impedance of an RC circuit is given by
$Z = \sqrt {{R^2} + {X_C}^2} $
Where,
$Z$ is the impedance
$R$ is the resistance
${X_C}$ is the capacitive reactance
We have the resistance as $R = 500\Omega $ and the capacitive reactance will be ${X_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{377 \times 2 \times {{10}^{ - 6}}}} = 1326.25\Omega $.
Substituting these values, we have the impedance as
$\eqalign{
  & Z = \sqrt {{R^2} + {X_C}} \cr
  & \Rightarrow Z = \sqrt {{{\left( {500} \right)}^2} + {{\left( {1326.25} \right)}^2}} \cr
  & \Rightarrow Z = 1417.37\Omega \cr} $
The peak current in the circuit will be given by
${i_0} = \dfrac{{{V_0}}}{Z} = \dfrac{{282}}{{1417.37}} = 0.199A$
The power factor will be
$\cos \phi = \dfrac{R}{Z} = \dfrac{{500}}{{1417.37}} = 0.353$
Now, from all these quantities, we have the Power of the RC circuit as
$\eqalign{
  & P = {i_{rms}}{V_{rms}}\cos \phi \cr
  & \Rightarrow P = \dfrac{{{i_0}}}{{\sqrt 2 }} \times \dfrac{{{V_0}}}{{\sqrt 2 }} \times \cos \phi \cr
  & \Rightarrow P = \dfrac{{0.199}}{{\sqrt 2 }} \times \dfrac{{282}}{{\sqrt 2 }} \times 0.353 \cr
  & \Rightarrow P = 9.9W \simeq 10W \cr
  & \therefore P = 10W \cr} $
Therefore, the power in the RC circuit is 10W.

So, the correct answer is “Option C”.

Note:
You must notice that capacitive reactance will have the same units as resistance. Also remember that peak value of voltage or current will always be the $\sqrt 2 $ times the rms value. Here you must notice that capacitors or inductors do not dissipate any power, so the true power is only due to resistance. One must make a note that the power factor is actually the ratio of true power to apparent power.