Question

In a group of children 45 play football, out of which 30 play football only, 28 play hockey, 25 play cricket, out of which 11 play cricket only. Further 7 play cricket and football but not hockey. 5 play football and hockey but not cricket and 10 play football and cricket both.
Represent the following in a Venn diagram and find :
1) How many children play all the three games?
2) How many children play hockey only?
3) How many children are there in the group?
4) What is the use of playing sports in our daily life?

Answer 1

Hint:
Here we have to first draw a Venn diagram and then we have to determine the number of children playing a particular game or two games or all three games. For the Venn diagram, we will first draw three circles of football, cricket and hockey. Then we will overlap the circles according to the given data. Then we will answer the rest of the questions with the help of the Venn diagram drawn.

Complete step by step solution:
Let’s write the given data first.
Total number of children plays football along with other games\[ = 25\]
Number of children plays football only \[ = 30\]
Number of children plays football and cricket\[ = 7\]
Number of children plays football and hockey\[ = 5\]
Therefore, Number of children plays football, cricket and hockey\[ = 45 - \left( {30 + 7 + 5} \right) = 3\]
Total number of children plays cricket along with other games\[ = 25\]
Number of children plays cricket only \[ = 11\]
Number of children plays football and cricket\[ = 7\]
Number of children plays football, cricket and hockey\[ = 3\]
Therefore, Number of children plays cricket and hockey\[ = 25 - \left( {11 + 7 + 3} \right) = 4\]
Total number of children plays hockey along with other games\[ = 28\]
Number of children plays hockey and cricket\[ = 4\]
Number of children plays hockey and football\[ = 5\]
Number of children plays football, cricket and hockey\[ = 3\]
Therefore, Number of children plays hockey only\[ = 28 - \left( {4 + 3 + 5} \right) = 16\]
Now we will draw the Venn Diagram.

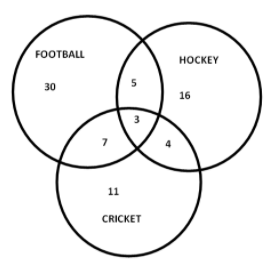
From the Venn Diagram, we can see that only 3 overlaps all the three games
Number of children plays all the three games\[ = 3\]

Number of children plays hockey only \[ = 16\]
Total number of children
\[ = \](football only\[ + \]cricket only \[ + \] hockey only) +(hockey and football\[ + \] hockey and cricket \[ + \]cricket and football) \[ + \] (football\[\]cricket\[ + \] hockey)
\[ = \left( {30 + 16 + 11} \right) + \left( {7 + 5 + 4} \right) + 3\]

After simplification, we get
Total number of children \[ = {\rm{ 76}}\]
Benefits of playing sports in our daily life are:-
We can maintain our weight by playing sports.
Sports reduce the chances of breast cancer in our life.
It makes us fit and healthy.

Note:
Here we have drawn a Venn diagram to represent the number of children in different games. A Venn diagram is a way of representing different groups of things using circles. If the circles overlap then it shows the commonality between these groups otherwise not. It is an easy way to find out the number of people enrolled in different activities.