Question

In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?

Answer 1

Hint: We can consider the people who can speak Hindi as a set and people who can speak English as another set. Then the union of these sets are the people who can speak at least one of the two languages, and their intersection gives the set of people who can speak both Hindi and English. Then we can find the number of people who can speak both languages using the equation $n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right)$.

Complete step by step solution: Consider H as the set of people who can speak Hindi. Then number of people who can speak Hindi is given by, $n\left( H \right) = 250$
Consider E as the set of people who can speak English. Then number of people who can speak English is given by, $n\left( E \right) = 200$
We can assume that out of 400 peoples, all of them can speak either English or Hindi.
$ \Rightarrow H \cup E$ is the union of sets H and E. Their number is given by, $n\left( {H \cup E} \right) = 400$
We can draw a Venn diagram with the given details for better understanding.

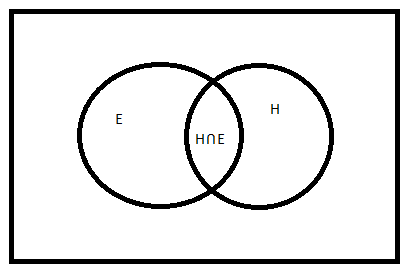
Here, curves E and H represent the sets of people who can speak English and can speak Hindi respectively. The overlapping region is the intersection of the 2 sets and the union of the set is given by the region of both the circle.
Now we need to find the number of people who can speak both English and Hindi. These people who can speak both belong to the intersection of H and E which is represented by $H \cap E$. Then we need to find $n\left( {H \cap E} \right)$
We know that, $n\left( {H \cap E} \right) = n\left( H \right) + n\left( E \right) - n\left( {H \cup E} \right)$
Substituting the values in the equation, we get,
$n\left( {H \cap E} \right) = 250 + 200 - 400$
On solving we get,
$ \Rightarrow n\left( {H \cap E} \right) = 50$

Therefore, the number of people who can speak both Hindi and English is 50.

Note: The concept used here is set theory. Union of two sets gives a set of all elements that are at least in one of the two sets. If A and B are 2 sets, then its union is written as $A \cup B$ and it contains all the elements in A along with all the elements in B. Intersection of two sets gives the set of all elements that are in both the sets. If A and B are 2 sets, then its intersection is written as $A \cup B$ and it contains all the elements that are both in A and B. The order of the set is not important while taking the union or intersection.
Venn diagram is used to represent sets. It helps us to understand sets, its union and intersection and other set operations. In a Venn diagram, each set is separated by a circle or a curve. The elements inside each curve belong to that particular set. If the curves are overlapping means that the elements are contained in all the overlapping sets. The Venn diagram is enclosed in a rectangle which represents the universal set.