Question

In a circle of radius 21 cm, an arc subtends an angle of \[{60^\circ}\] at the centre. Find
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) The area of the segment made by this arc.

Answer 1

Hint: First of all, draw the neat diagram for every sub question to get an idea of what we have to find. The area of the segment made by the arc is given by the difference of the areas of the sector formed by the arc and the triangle formed by the segment of the arc. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
Given radius of a circle \[r = 21{\text{ cm}}\]
Angle subtended by an arc \[\theta = {60^\circ}\]

 (i) The length of the arc
We know that the length of the arc of a circle with radius \[r\] and subtended by an angle \[\theta \] is given by \[\dfrac{\theta }{{{{360}^\circ}}} \times \left( {2\pi r} \right)\]

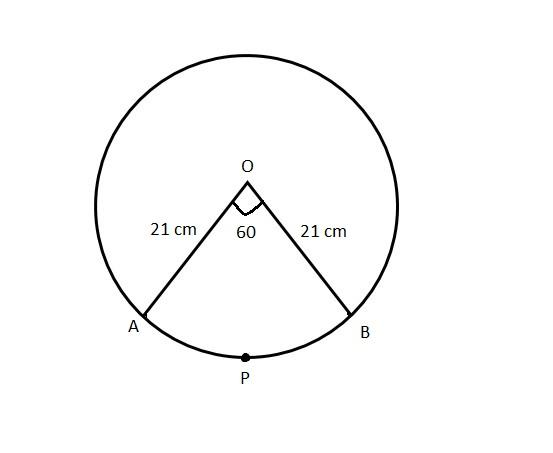
So, the length of the arc \[APB = \dfrac{\theta }{{{{360}^\circ}}} \times \left( {2\pi r} \right)\]
                                                      \[
   = \dfrac{{{{60}^\circ}}}{{{{360}^\circ}}} \times 2 \times \pi \times 21 \\
   = \dfrac{1}{6} \times 2 \times \dfrac{{22}}{7} \times 21 \\
   = 22{\text{ cm}} \\
\]

(ii) Area of the sector formed by the arc
We know that the area of a sector formed by the arc of a circle with radius \[r\] and subtended by an angle \[\theta \] is given by \[\dfrac{\theta }{{{{360}^\circ}}} \times \pi {r^2}\]

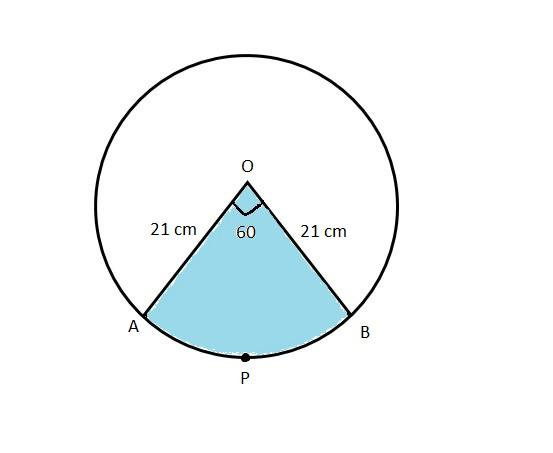
So, area of the sector OAPB \[ = \dfrac{\theta }{{{{360}^\circ}}} \times \pi {r^2}\]
                                                   \[
   = \dfrac{{{{60}^\circ}}}{{{{360}^\circ}}} \times \pi {\left( {21} \right)^2} \\
   = \dfrac{1}{6} \times \dfrac{{22}}{7} \times 21 \times 21 \\
   = \dfrac{1}{3} \times 11 \times 3 \times 21 \\
   = 231{\text{ c}}{{\text{m}}^2} \\
\]

 (iii) The area of the segment made by this arc.
We know that the area of the segment formed by the arc of a circle with radius \[r\] and subtended by an angle \[\theta \] is given by the difference of the area of the sector and area of the triangle formed by the chord of the segment.

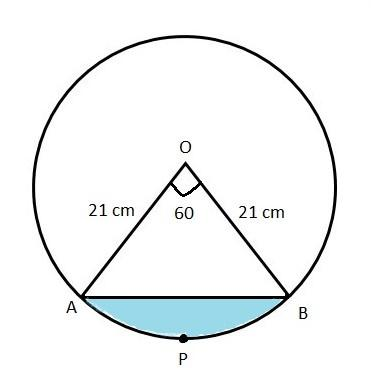
From the figure, clearly \[\Delta AOB\] is an isosceles triangle.
We know that the area of an isosceles triangle with equal sides of length \[a\] and their corresponding angle \[\theta \] between them is given by \[\Delta = \dfrac{1}{2}{a^2}\sin \theta \]
So, the area of the \[\Delta AOB\] is given by
\[
   \Rightarrow \Delta = \dfrac{1}{2}{\left( {21} \right)^2}\sin {60^\circ} \\
   \Rightarrow \Delta = \dfrac{1}{2}\left( {21 \times 21 \times \dfrac{{\sqrt 3 }}{2}} \right) \\
  \therefore \Delta = \dfrac{{441\sqrt 3 }}{4}{\text{ c}}{{\text{m}}^2} \\
\]
The area of segment APB = Area of sector OAPB – Area of \[\Delta AOB\]
                                           \[ = \left( {231 - \dfrac{{441\sqrt 3 }}{4}} \right){\text{ c}}{{\text{m}}^2}\]

Note: The length of the arc of a circle with radius \[r\] and subtended by an angle \[\theta \] is given by \[\dfrac{\theta }{{{{360}^\circ}}} \times \left( {2\pi r} \right)\]. The area of a sector formed by the arc of a circle with radius \[r\] and subtended by an angle \[\theta \] is given by \[\dfrac{\theta }{{{{360}^\circ}}} \times \pi {r^2}\]. The area of an isosceles triangle with equal sides of length \[a\] and their corresponding angle \[\theta \] between them is given by \[\Delta = \dfrac{1}{2}{a^2}\sin \theta \].