
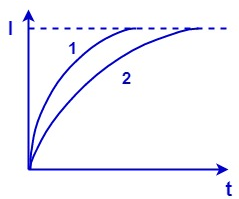
In a certain circuit consisting of a constant e.m.f. E, an inductance L and a resistance R is closed, the current in it increases with time according to curve 1. After one parameter (E, L or R) is changed the increase in current follows curve 2, when the circuit is closed second time. Which parameter was changed and in what direction?

Answer
549.9k+ views
Hint
Use the slope of the given graph to know which one is more or less and then using the formula of self-inductance we can find its proportionality with the slope and hence we can know what changes have occurred in the parameters. Here,
$ L\text{ }\alpha \text{ }\dfrac{1}{\dfrac{dI}{dt}} $
Self inductance is defined as the induction of a voltage in a current carrying wire when the current in the wire itself is changing. Self induction is the way in which single coils and chokes operate.
Complete step by step solution
Here, slope of the graph is $ \dfrac{dI}{dt} $
We can clearly see from the given graph that
Slope of curve 1 > slope of curve 2 i.e.
$ {{\left( \dfrac{dI}{dt} \right)}_{1}}>{{\left( \dfrac{dI}{dt} \right)}_{2}} $
As we know,
$ V=L\dfrac{dI}{dt} $
We can clearly see that L is inversely proportional to $ \dfrac{dI}{dt} $ i.e.
$ L\text{ }\alpha \text{ }\dfrac{1}{\dfrac{dI}{dt}} $
Now if slope i.e. $ \dfrac{dI}{dt} $ is decreasing along the curve 2 that means that the self-inductance i.e. L is increasing here.
Or we can say
$ {{L}_{2}}>{{L}_{1}} $
Hence, the changed parameter here is self-inductance L which has increased during the increase in current along the curve 2.
Note
Remember that the self-inductance is directly proportional to $ \dfrac{dt}{dI} $ which is the inverse of the slope in the given figure. Had there been the graph of time vs current with the same curves, the self-inductance would have been said to decrease with the decrease in slope of curve 2.
Use the slope of the given graph to know which one is more or less and then using the formula of self-inductance we can find its proportionality with the slope and hence we can know what changes have occurred in the parameters. Here,
$ L\text{ }\alpha \text{ }\dfrac{1}{\dfrac{dI}{dt}} $
Self inductance is defined as the induction of a voltage in a current carrying wire when the current in the wire itself is changing. Self induction is the way in which single coils and chokes operate.
Complete step by step solution

Here, slope of the graph is $ \dfrac{dI}{dt} $
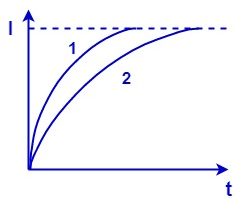
We can clearly see from the given graph that
Slope of curve 1 > slope of curve 2 i.e.
$ {{\left( \dfrac{dI}{dt} \right)}_{1}}>{{\left( \dfrac{dI}{dt} \right)}_{2}} $
As we know,
$ V=L\dfrac{dI}{dt} $
We can clearly see that L is inversely proportional to $ \dfrac{dI}{dt} $ i.e.
$ L\text{ }\alpha \text{ }\dfrac{1}{\dfrac{dI}{dt}} $
Now if slope i.e. $ \dfrac{dI}{dt} $ is decreasing along the curve 2 that means that the self-inductance i.e. L is increasing here.
Or we can say
$ {{L}_{2}}>{{L}_{1}} $
Hence, the changed parameter here is self-inductance L which has increased during the increase in current along the curve 2.
Note
Remember that the self-inductance is directly proportional to $ \dfrac{dt}{dI} $ which is the inverse of the slope in the given figure. Had there been the graph of time vs current with the same curves, the self-inductance would have been said to decrease with the decrease in slope of curve 2.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

When was the first election held in India a 194748 class 12 sst CBSE




