Question

If $x={{\sin }^{-1}}\left( \sin 10 \right)$ and $y={{\cos }^{-1}}\left( \cos 10 \right)$ then $y-x=$?
(a) $\pi $
(b) 0
(c) $\pi -20$
(d) $2\pi $

Answer 1

Hint: Here, first let us draw the graph and mention which trigonometric functions are positive in which quadrant. Use the basic principles of sine and cosine functions and the angle in which they are positive. Convert the given angle into the obtained angle and then use basic operation of subtraction to find the result.

Complete step-by-step answer:
Here, we have been given $x={{\sin }^{-1}}\left( \sin 10 \right)$ and $y={{\cos }^{-1}}\left( \cos 10 \right)$. Let us first draw a graph and the significance of trigonometric functions in the graph.

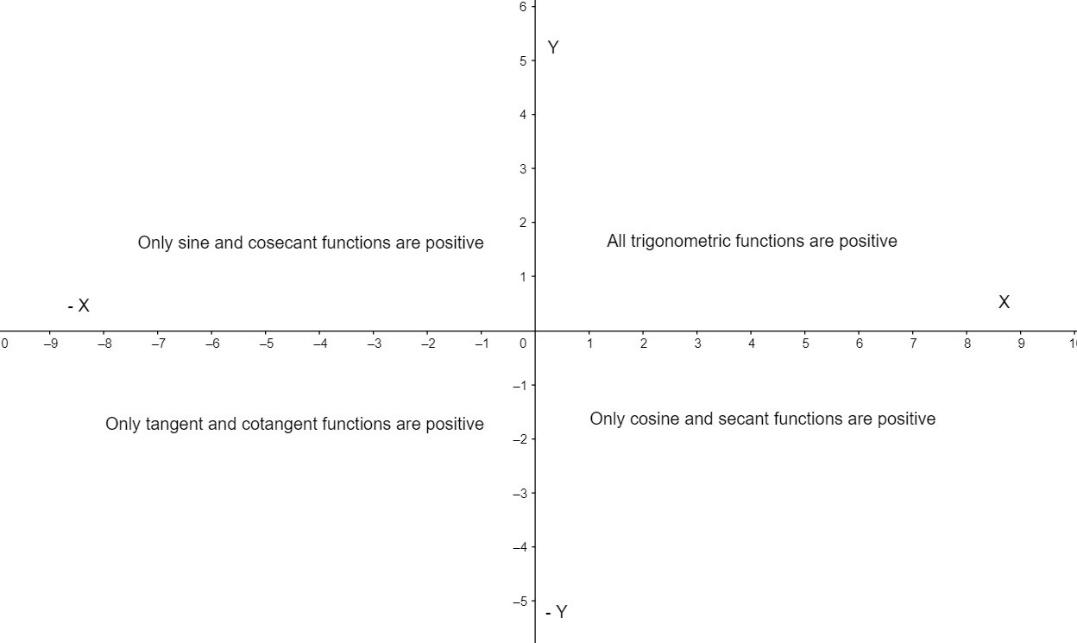
From the given values, we can see that in sin (10) and cos (10) has no value because ${{\sin }^{-1}}x$ $\in \left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)$, hence we shall find the value of $x$. Also, $\pi $ = 3.141.
Now, we know that the sine function is positive in 1^st and 2^nd quadrant, and hence, sine function is positive for $\pi -\theta $, $2\pi +\theta $ and $3\pi -\theta $. We know, $\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)=\left( -1.57,\,1.57 \right)$
For, $\pi -10$:
$\pi -10$ = 3.141 – 10 = – 6.85, this does not lie within $\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)$
For, $2\pi +10$:
$2\pi +10$ = 2 (3.141) + 10 = 16.28, this does not lie within $\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)$
For, $3\pi -10$:
$3\pi -10$ = 3 (3.141) – 10 = – 0.57, this lies within $\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)$
Therefore, we can write sin (10) as sin ($3\pi -10$).
Now, $x={{\sin }^{-1}}\left[ \sin \left( 3\pi -10 \right) \right]$
We get, $x=3\pi -10$…………. (1)
Now, let us find the value of $y$,
For cosine functions, we can see that cosine is only positive in the 4^th quadrant and 1^st quadrant. Since cosine is an even function we can use 0, $2\pi $, $4\pi $. We know that, ${{\cos }^{-1}}$$\in \left( -\pi ,\,\,\pi \right)$. We will get cosine as positive in $2\pi -\theta $, $2\pi +\theta $, $4\pi -\theta $. $\left( -\pi ,\,\,\pi \right)=\left( -3.141,\,\,3.141 \right)$
For, $2\pi -\theta $:
$2\pi -\theta $ = 2 (3.141) – 10 = – 3.71 does not lie within $\left( -\pi ,\,\,\pi \right)$.
For, $2\pi +\theta $:
$2\pi +\theta $ = 2 (3.141) + 10 = 16.28 does not lie within $\left( -\pi ,\,\,\pi \right)$.
For, $4\pi -\theta $:
$4\pi -\theta $ = 4 (3.141) – 10 = 2.564, this lies within $\left( -\pi ,\,\,\pi \right)$.
Therefore, we can write cos (10) as cos ($4\pi -10$).
Now, $y={{\cos }^{-1}}\left[ \cos \left( 4\pi -10 \right) \right]$
We get, $y=4\pi -10$........... (2)
Subtract equation (1) from equation (2), we get
$\begin{align}
  & y-x=\left( 4\pi -10 \right)-\left( 3\pi -10 \right) \\
 & =4\pi -10-3\pi +10 \\
 & =\pi
\end{align}$
Hence, the value of $y-x$ is $\pi $

Note: In this question, to determine the nature of the sign of the trigonometric functions when its angle is in which quadrant is important because the whole solution depends on it. Also, the even function means $f\left( -x \right)=f\left( x \right)$ and odd functions are $f\left( -x \right)=-f\left( x \right)$.