Question

If we are given \[\overline{GH}\cong \overline{GJ}\] and \[HI=12\], what is \[IJ\]?

Answer 1

Hint: Here, in this problem, a figure is given. If you notice this figure then you can notice that a perpendicular line is divided into two equal parts. That means here we require the concept of perpendicular bisector theorem which says that \[HI=IJ\]. Hence, we can say that \[IJ=12\] because \[HI=12\].

Complete step-by-step solution:
Before, starting the problem first of all we need to know about perpendicular bisector theorem and its proof then it becomes easier to understand the problem
First of all, we need to understand the concept of perpendicular bisector theorem
The perpendicular bisector is a line segment that is perpendicular to the triangle's side or cuts the side into two equal parts, passing through the middle of the triangle's side.
Figure of triangle of perpendicular bisector is given below:

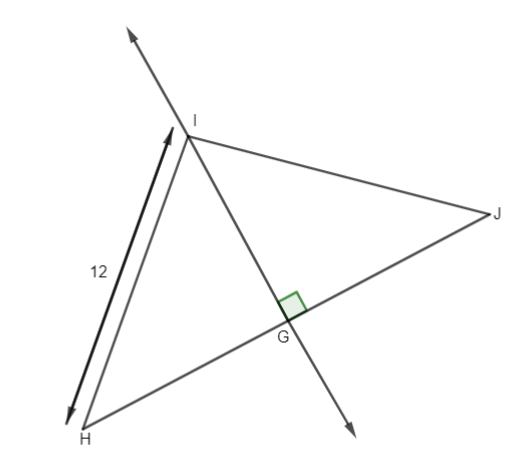
From this figure we can notice that Line IG is perpendicular bisector to HJ
So, \[\angle HGI=\angle IGJ={{90}^{\circ }}--(1)\]
The line IG which bisects line HJ as it is a perpendicular bisector.
\[GH=GJ--(2)\]
therefore, we can say that \[\overline{GH}\cong \overline{GJ}\]
From the given figure,
In \[\Delta IGH\]and \[\Delta IGJ\]
From the common sides of the triangle that is
\[IG=IG\] (Common sides of a triangle)
From the equation (1) we get:
\[\angle IHG=\angle IJG\]
From the equation (2) we get:
\[GH=GJ\]
Therefore, by SAS congruence rule - By SAS rule, the two supplied triangles are said to be congruent if any two sides and the included angle between the sides of one triangle are comparable to the corresponding two sides and the included angle between the sides of the second triangle.
Hence, \[\Delta IGH\cong \Delta IGJ\]
By the principle of corresponding parts of congruent triangles (CPCT), which asserts that if two or more triangles are obtained, the corresponding angles and sides of the specified triangles are also congruent.
\[\therefore HI=IJ---(3)\]
Now, we come to the question it is given the value of \[HI=12\] substitute this value on equation (3) we get:
\[IJ=12\]
So, the correct answer is \[IJ=12\].

Note: Always remember that while solving this type of problem, following all the conditions to prove this perpendicular bisector, we can easily understand the value of \[IJ\]. SSS criteria (Side - Side - Side), SAS criteria (Side – Angle - Side), ASA criteria (Angle – Side – Angle), AAS criteria (Angle – Angle – Side), RHS criteria (Right angle – Hypotenuse – Side) above mentioned the conditions are important to solve similar types of problem.