Question

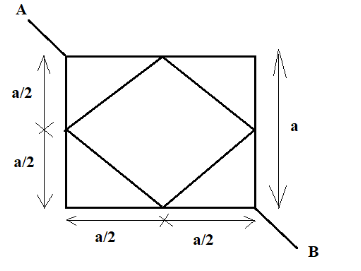
If the wire has resistivity \[\rho \], find the resistance between \[{\text{A}}\] and \[{\text{B}}\].

Answer 1

Hint: First of all, we will find the slanting length of the figure inside. We will use a resistance formula which relates resistivity, length and cross-sectional area of the wire. If the current divides at a junction, then they are connected in parallel. Current does not flow under the same potential.

Complete step by step answer:
In the given question, we are supplied with the following information:
There is a mesh of wire, whose resistivity is \[\rho \].
The area of the cross section of the wire is \[A\].
We are required to find the equivalent resistance between \[{\text{A}}\] and \[{\text{B}}\].

To begin with, we will draw the diagram for better understanding.

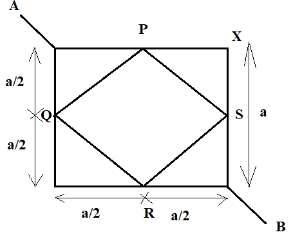
In the diagram, we can find the length of the part \[{\text{PQ}}\] by using Pythagoras theorem. In the triangle \[{\text{APQ}}\], we have,
$P{Q^2} = A{Q^2} + A{P^2} \\
\Rightarrow P{Q^2} = {\left( {\dfrac{a}{2}} \right)^2} + {\left( {\dfrac{a}{2}} \right)^2} \\
\Rightarrow PQ = \dfrac{a}{{\sqrt 2 }} $

Now, we have to find the total length of the wire such that we can calculate the net resistance of it.In the figure, it can be seen that the potential at the point \[P\] and \[Q\] are equal. Hence, there is no flow of current through that arm \[PQ\].Similarly, we can also say that there will be no current flowing in the arm \[RS\]. Now, we will need to find out the resistance of each arm.
${R_{AP}} = \dfrac{{\rho \times \dfrac{a}{2}}}{A} \\
\Rightarrow {R_{AP}} = \dfrac{{\rho a}}{{2A}}$

As we can see that the arm \[PXS\] is parallel to the arm \[PS\], so we can easily calculate the net resistance, by using the formula of parallel resistors.
$\dfrac{1}{{{R_1}}} = \dfrac{1}{{{R_{PXS}}}} + \dfrac{1}{{{R_{PS}}}} \\
\Rightarrow \dfrac{1}{{{R_1}}} = \dfrac{1}{{\dfrac{{\rho \times a}}{A}}} + \dfrac{1}{{\dfrac{{\rho \times a}}{{\sqrt 2 A}}}} \\
\Rightarrow \dfrac{1}{{{R_1}}} = \dfrac{A}{{\rho a}} + \dfrac{{\sqrt 2 A}}{{\rho a}} \\
\Rightarrow {R_1} = \dfrac{{\rho a}}{{A\left( {\sqrt 2 } \right) + 1}}$

Now, we can find the net resistance of the arms \[AP\], \[PXS\], \[PS\] and \[SB\] as they are in series connection now.
${R_2} = {R_{AP}} + {R_1} + {R_{SB}} \\
\Rightarrow {R_2} = \dfrac{{\rho a}}{{2A}} + \dfrac{{\rho a}}{{A\left( {\sqrt 2 } \right) + 1}} + \dfrac{{\rho a}}{{2A}} \\
\Rightarrow {R_2} = \dfrac{{\rho a}}{A}\left( {1 + \dfrac{1}{{1 + \sqrt 2 }}} \right) \\
\Rightarrow {R_2} = \dfrac{{\rho a\left( {\sqrt 2 + 2} \right)}}{{A\left( {\sqrt 2 + 1} \right)}}$

Similarly, the net resistance of the arm \[AQ\], \[QR\], \[QYR\] and \[RB\] is also:
${R_3} = \dfrac{{\rho a\left( {\sqrt 2 + 2} \right)}}{{A\left( {\sqrt 2 + 1} \right)}}$.
Now, we will find the net resistance of both the arms which are in parallel.
$\dfrac{1}{{{R_{{\text{eq}}}}}} = \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} \\
\Rightarrow \dfrac{1}{{{R_{{\text{eq}}}}}} = \dfrac{1}{{\dfrac{{\rho a\left( {\sqrt 2 + 2} \right)}}{{A\left( {\sqrt 2 + 1} \right)}}}} + \dfrac{1}{{\dfrac{{\rho a\left( {\sqrt 2 + 2} \right)}}{{A\left( {\sqrt 2 + 1} \right)}}}} \\
\Rightarrow {R_{{\text{eq}}}} = \dfrac{{\rho a\left( {\sqrt 2 + 2} \right)}}{{2A\left( {\sqrt 2 + 1} \right)}} \\
\Rightarrow {R_{{\text{eq}}}} = \dfrac{{\rho a}}{{\sqrt 2 A}}$

Hence, the equivalent resistance is \[\dfrac{{\rho a}}{{\sqrt 2 A}}\].

Note: While solving this problem, we should remember that current does not flow under the same potential difference. In case of series connection, current flow through the elements remains the same. While in the parallel connection, the voltage of all the elements remains the same.