Question

If the number of radical axes formed out of a given number of circles be the same as the number of radical centres, then find the number of given circles.

Answer 1

Hint: To solve this question, firstly we will find the number of ways of selecting 2 circles out of n circles for radical axis and number of ways of selecting 3 circles out of n circles. Then, using the condition given in question, we will put $^{n}{{C}_{2}}{{=}^{n}}{{C}_{3}}$, and solve for value of n, which is number of circles.

Complete step-by-step answer:
Now, before we solve the question, first let us see what is the meaning of radical axis and radical centre.
Radical Axis is also known as power axis. Radical axis of two non- concentric circles is defined by the two circles, perpendicular to the line connecting the centres of the circles.

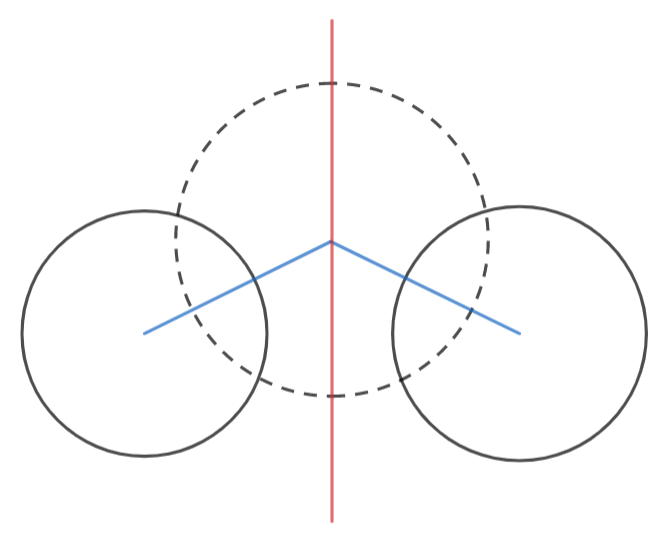
In figure, the red line shows the radical axis for the two circles with boundary in solid black.
Radical centres are also called power centres. Radical centre is the intersection point of the three radical axes of the pairs of circles.

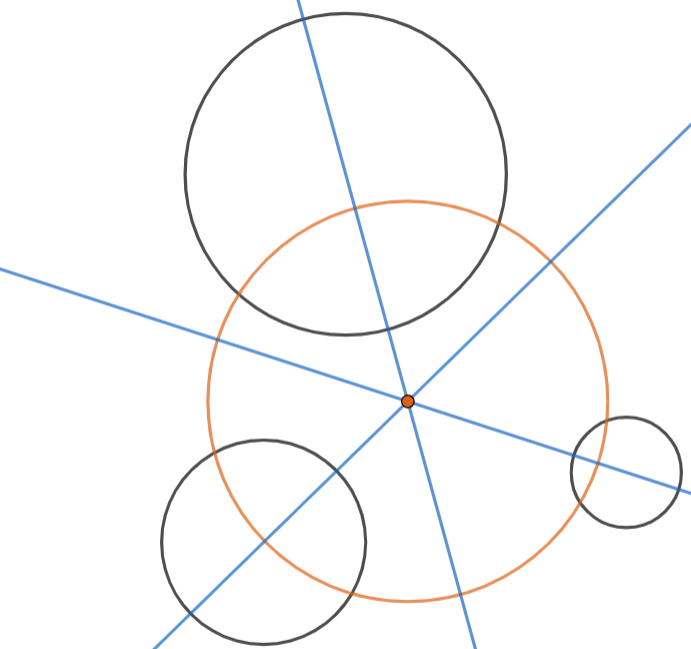
Here, in figure, the radical centre is the orange point of a unique circle in solid orange border, cutting the other three circles at right angles.
Now, let's move toward the question.
Let the number of circles be equals to n. We know that the radical axis is obtained by taking two circles at a time and the radical centre is obtained by taking 3 circles at a time.
So, number of Radical Axis out of n circles we have $^{n}{{C}_{2}}$ and number of Radical centre out of n circles we have $^{n}{{C}_{3}}$.
Now, in question it is given that the number of radical axes formed out of a given number of circles be the same as the number of radical centres.
So, $^{n}{{C}_{2}}{{=}^{n}}{{C}_{3}}$
We know that, $^{n}{{C}_{r}}=\dfrac{n!}{r!(n-r)!}$, which gives the value of number of ways of selecting r items from total n items, where n > r.
So, we have
$\dfrac{n!}{2!(n-2)!}=\dfrac{n!}{3!(n-3)!}$
As, we know that $n!=n(n-1)(n-2).....3.2.1$ , where n > 0
So, on simplification, we get
$\dfrac{1}{2(n-2)(n-3)!}=\dfrac{1}{3.2(n-3)!}$
On solving, we get
$\dfrac{1}{(n-2)}=\dfrac{1}{3}$
Using, cross multiplication we get
n – 2 = 3
or, n = 5
Hence, the number of given circles is equal to 5.

Note: Always remember that $^{n}{{C}_{r}}=\dfrac{n!}{r!(n-r)!}$, where the formula gives the number of ways of selecting r items from total n items, where n > r. Also, remember that $n!=n(n-1)(n-2).....3.2.1$ , where n > 0. Also, remember that the radical axis is obtained by taking two circles at a time and the radical centre is obtained by taking 3 circles at a time. Try not to make any calculation mistakes.